Рассмотрим уравнение инверсии для стационарного случая.
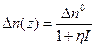 , где
, где 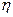 - параметр насыщения
- параметр насыщения
- закон насыщения инверсии, 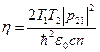 ,
, 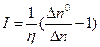
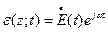 - поле,
- поле, 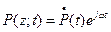
Усреднение по резонатору (пространственное):
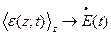
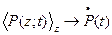 - точечная модель лазера.
- точечная модель лазера.
Рассмотрим одночастотный режим (одномодовый)
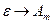 - одна амплитуда
- одна амплитуда
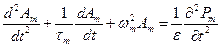
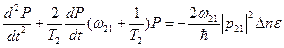
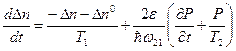 , где
, где 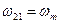 ,
, 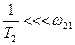
Перейдем к комплексным амплитудам:
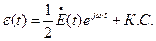
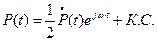
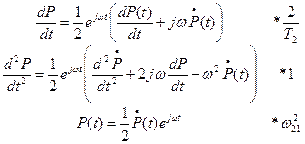
Максимальная скорость изменения поляризации: 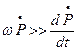 -изменение амплитуды во времени.
-изменение амплитуды во времени.
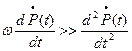 Приближение малости приводит к тому, что вторая производная уходит.
Приближение малости приводит к тому, что вторая производная уходит.
Т.О.остается уравнение 1 порядка (укороченное уравнение для поляризации)
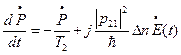 (I) (I)
|
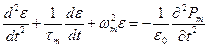
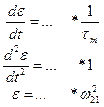
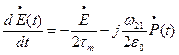
|
Процедура вычисления 1-й производной, 2-й производной и получение уравнения – аналогичная.
Либо можно воспользоваться укороченным уравнением, где 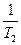 заменить на
заменить на 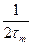 ,
, 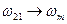
Уравнение для инверсии:
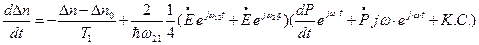
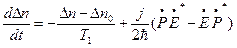
См. уравнение (I), 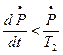 , подставляем в предыдущее уравнение
, подставляем в предыдущее уравнение 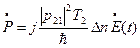
Воспользовавшись этим выражением в правой части для инверсии вместо PP* получили ЕЕ*- величину, связанную с интенсивностью.
Для записи конечных уравнений удобным является язык фотонов в резонаторе.
Число фотонов в резонаторе:
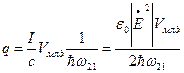 , где
, где 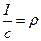
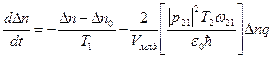
Воспользуемся записанным выше выражением для B21: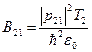
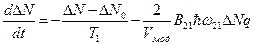
Необходимо получить уравнение для числа фотонов в резонаторе
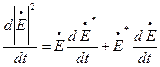 ,
, 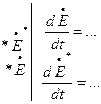 +
+
Воспользовавшись уравнением 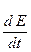 :
:
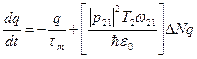 , или
, или 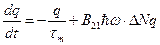
Где 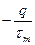 - отвечает за потери фотонов,
- отвечает за потери фотонов, 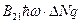 - характеризует появление фотонов за счет вынужденного испускания.
- характеризует появление фотонов за счет вынужденного испускания.
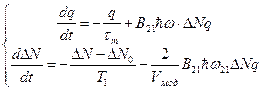
Плотность энергии 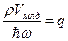
Уравнения для числа фотонов в резонаторе и инверсии населенностей можно получить более коротким путем.
Для двухуровневой системы. Кинетическая схема:

| B21ρ – индуцированное испускание. А21 –вероятность перехода части с 2 на 1 (спонтанные переходы) B12ρ- резонансное поглощение B21= B12 |
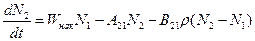 -кинетическое уравнение, отвечает за населенность.
-кинетическое уравнение, отвечает за населенность.
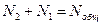 - общее чисто частиц.
- общее чисто частиц.
Аналогично, 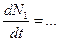 ,
, 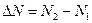
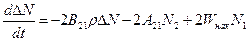
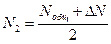 ,
, 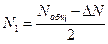
Подставляем N2 и N1 в уравнение для инверсии:
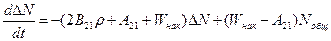
В стационарном состоянии в отсутствии генерации 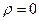
Из этого уравнения будет вытекать:
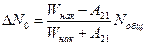 (
(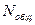 - зависит от параметров лазера)
- зависит от параметров лазера)
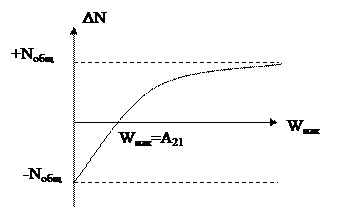
Проведя алгебраические преобразования:
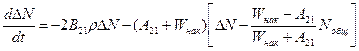
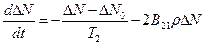
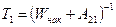 - время продольной релаксации.
- время продольной релаксации.
Если есть порог:

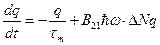 , условие начала генерации
, условие начала генерации 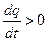 =>
=> 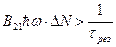
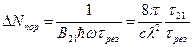
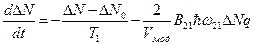 - исходное уравнение, которое должны были вывести.
- исходное уравнение, которое должны были вывести.
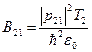 ,
, 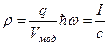 ,
, 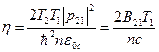 - параметр насыщения
- параметр насыщения
 2014-02-03
2014-02-03 547
547







