Доказательство. По теореме Лагранжа: f(x) – f(x1) = f¢(e)(x – x1), где x < e < x1

Пусть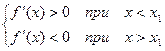

По теореме Лагранжа: f(x) – f(x₁) = f¢(e)(x – x₁), где x < e < x₁.

Тогда: 1) Если х < x₁, то e < x₁; f¢(e)>0; f¢(e)(x – x₁)<0, следовательно

f(x) – f(x₁)<0 или f(x) < f(x₁).

2) Если х > x₁, то e > x₁ f¢(e)<0; f¢(e)(x – x₁)<0, следовательно

f(x) – f(x₁)<0 или f(x) < f(x₁).

Т. к. ответы совпадают, то можно сказать, что f(x) < f(x₁) в любых точках вблизи х₁, т.е. х₁ – точка максимума.

Доказательство теоремы для точки минимума производится аналогично.

Теорема доказана.

На основе вышесказанного можно выработать единый порядок действий при нахождении наибольшего и наименьшего значения функции на отрезке:

1) Найти критические точки функции.

2) Найти значения функции в критических точках.

3) Найти значения функции на концах отрезка.

4) Выбрать среди полученных значений наибольшее и наименьшее.

Исследование функции на экстремум с помощью

производных высших порядков.

Пусть в точке х = х₁ f¢(x₁) = 0 и f¢¢(x₁) существует и непрерывна в некоторой окрестности точки х₁.

Теорема. Если f¢(x₁) = 0, то функция f(x) в точке х = х₁ имеет максимум, если f¢¢(x₁)<0 и минимум, если f¢¢(x₁)>0.