Тригонометрическая форма комплексного числа. Абсциссу a и ординату b комплексного числа a + bi можно выразить через его модуль r и аргумент 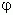 :
:
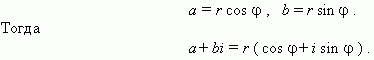
Показательная и тригонометрические функции в области комплексных чисел связаны между собой формулой
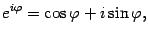 |
которая носит название формулы Эйлера.
Пусть комплексное число 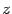 в тригонометрической форме имеет вид
в тригонометрической форме имеет вид 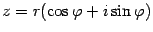 . На основании формулы Эйлера выражение в скобках можно заменить на показательное выражение. В результате получим
. На основании формулы Эйлера выражение в скобках можно заменить на показательное выражение. В результате получим
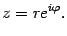
Эта запись называется показательной формой комплексного числа. Так же, как и в тригонометрической форме, здесь 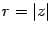
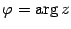 .
.
Пример. Пусть 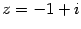 . Напишите показательную форму числа
. Напишите показательную форму числа 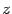 .
.
Решение. Находим модуль и аргумент числа:
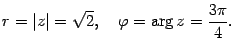
Следовательно, показательная форма комплексного числа такова:
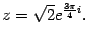
Пример. Комплексное число записано в показательной форме
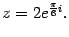
Найдите его алгебраическую форму.
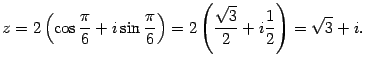
Итак, алгебраическая форма числа: 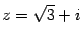 .
.
С помощью формулы Эйлера можно определить показательную функцию комплексного аргумента. Пусть 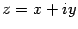 .
.
Тогда
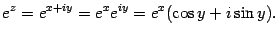
Например,
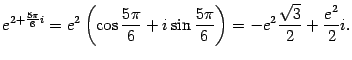
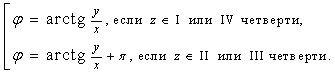
Изобразить на комплексной плоскости следующие числа и записать их в тригонометрической форме.
1) z = 1 + i
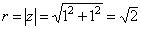 ,
,
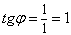 Þ
Þ 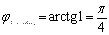
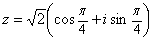 ;
;

2) 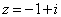
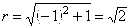 ,
,
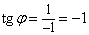 Þ
Þ 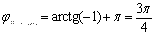
Þ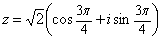 ;
;

3)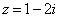 Þ
Þ
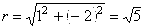 ,
,
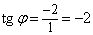 Þ
Þ
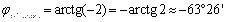 Þ
Þ
 ;
;

4)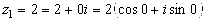 ,
,
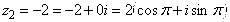 ;
;
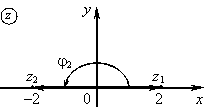
5)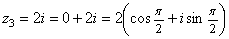 ,
,
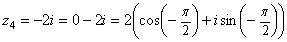 ;
;
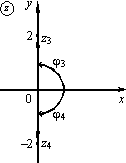
6)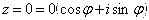 ,
,
то есть для z = 0 будет
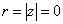 , j не определен.
, j не определен.
7)

8)
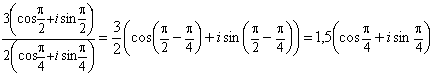 .
.
9)
Вычислить (1 + i)10.
Решение:

10)
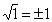 , так как
, так как 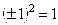 ;
;
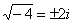 , так как
, так как 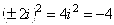 ;
;
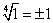 или
или 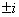 , так как
, так как 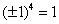 и
и 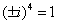 .
.
11)
1) 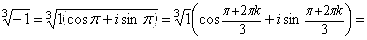
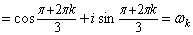 , k = 0, 1, 2
, k = 0, 1, 2
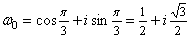 ,
,
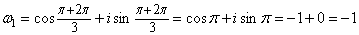 ,
,
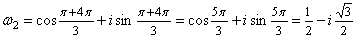 .
.
Ответ:
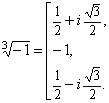
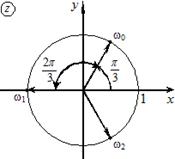
12)
1)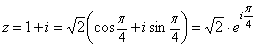 ;
;
2)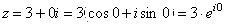 ;
;
3)  .
.
13)
Пусть 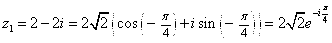 ,
,
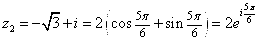 .
.
Тогда 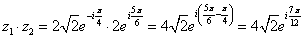 ;
;
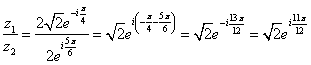 ;
;
 ;
;
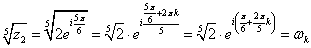 ,
, 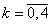

 2014-02-03
2014-02-03 10137
10137







