Государства

ТЕОРИЯ

Ограничение по мощности, или насыщение (рис.4.3).

Статическая характеристика линейной системы 1-2 имеет неравномерность регулирования Dлин. Вследствие нечувствительности в нелинейной системе регулируемая величина может находиться в зоне у±e, и при этом реакция регулятора отсутствует. Статическая характеристика нелинейной системы представляет собой область 3-4-6-5.Тогда неравномерность регулирования нелинейной системы как разность между наибольшим и наименьшим значениями регулируемой величины составляет Dнел, то есть при наличии мёртвой зоны неравномерность регулирования возрастает.

Рис.4.2. Влияние мёртвой зоны: увеличение неравномерности

регулирования.

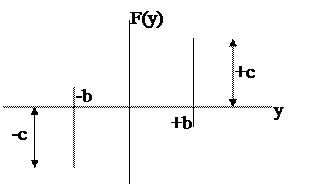Рис.4.3.Нелинейность типа насыщения.

y < -b Þ F(y) = -c;

-b £ y £ + b Þ F(y) = ky;

y > + b Þ F(y) = +c.

Нелинейные характеристики такого типа присущи обычно усилителям. Присутствие их обусловливает ограничение скорости срабатывания исполнительного механизма, а следовательно, увеличение продолжительности переходного процесса.

3.Характеристика типа «реле» (рис.4.4).

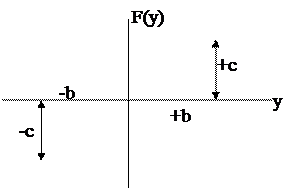Рис.4.4. Нелинейность типа «реле».

y < -b Þ F(y) = -c;

-b £ y £ +b Þ F(y) = 0;

y > +b Þ F(y) = +c.

Наличие такой нелинейной характеристики обусловливает часто незатухающие колебания регулируемой величины (например, работа холодильной установки с периодическими включением-выключением компрессора).

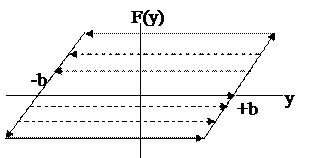4.Нелинейность типов «люфт» либо «сухое трение» (рис.4.5).

Рис.4.5. Нелинейность типа «люфт» либо «сухое трение».

py > 0 Þ F(y) = k(y-b);

py <0 Þ F(y) = k(y+b).

При наличии в системе элементов с такими характеристиками обычно ухудшаются многие показатели качества регулирования одновременно.

5.Всевозможные комбинации рассмотренных нелинейностей.

Не следует, однако, думать, что качество регулирования из-за наличия нелинейных звеньев обязательно ухудшается. Наоборот, во многих случаях удачное применение нелинейных элементов может позволить получить систему с весьма высоким качеством, не достижимым в линейной системе.

Звенья с показанными нелинейными характеристиками принципиально не могут быть представлены даже приближённо в виде линейных с использованием метода малых отклонений, поскольку этот метод предполагает возможность представления функции рядом Тейлора, что, в свою очередь, требует наличия у функции производных любого порядка. У рассмотренных функций в точках изломов не существует уже первых производных. Для терминологического выделения подобных нелинейностей к ним применяют термин «существенные нелинейности».

4.2. Основные отличия нелинейных систем от линейных.

1.Нелинейные системы не подчиняются принципу суперпозиции то есть для них

,

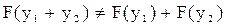поэтому решение дифференциального уравнения нелинейной САР не может быть представлено в виде суммы общего и частного решений, существует только полное решение.

2.В режиме вынужденных колебаний выходные колебания отличаются от входных не только амплитудой и фазой (как у линейных систем), но могут отличаться и по частоте.

3.В нелинейных системах возможно даже теоретически окончание переходного процесса за конечное время.

4.Нелинейным системам свойственно явление автоколебаний, когда в системе устанавливаются незатухающие колебания либо при входном воздействии неколебательного характера, либо вообще при отсутствии входного воздействия. Это явление не может быть объяснено с позиций линейного математического аппарата.

В то время, как аппарат линейной теории автоматического регулирования разработан достаточно полно и может быть с успехом применен в приложениях к линейным САР, для исследования нелинейных систем с получением точного конечного результата не существует общей теории, и во многих случаях требуется индивидуальный подход. Относительно неплохо разработаны приближённые методы анализа автоколебаний, расчеты же переходных процессов и синтез САР в настоящее время выполняются методами моделирования.

4.3. Автоколебания в нелинейных САР

и физическая картина их возникновения.

Явление автоколебаний наблюдается только в нелинейных системах. Внешне оно выражается в существовании режимов незатухающих колебаний и в некоторой степени является аналогом границы устойчивости линейных систем, однако имеет существенные отличия. Одно из них – в линейной системе, находящейся на границе устойчивости, преобразование кинетической энергии в потенциальную и обратно происходит без потерь, тогда как при автоколебаниях происходит рассеяние энергии, и её потери восполняются из каких-либо источников (объект регулирования либо регулятор непрямого действия, либо, наконец, внешняя среда). Для уяснения физической картины возникновения автоколебаний рассмотрим систему (рис.4.6), содержащую линейную часть с передаточной функцией W_л и нелинейный элемент типа «ограничение по мощности» c нелинейной характеристикой x = F(y).

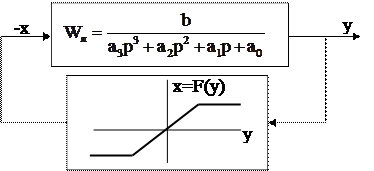Рис.4.6. Нелинейная САР.

Рассмотрим вспомогательную линейную систему (рис.4.7), имеющую вместо нелинейного элемента линейное звено с передаточной функцией W=k_л.

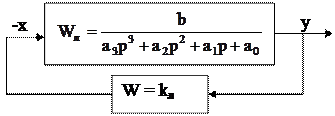Рис.4.7. Вспомогательная система.

Выполним анализ этой системы на устойчивость. Для этого найдём передаточную функцию замкнутой системы:

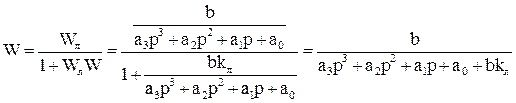. (4.2)

Характеристическое уравнение этой системы

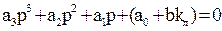. (4.3)

Применяя, например, критерий устойчивости Гурвица, можно сделать следующие заключения:

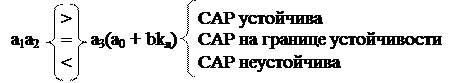
(4.4)

Отсюда можно сделать такие заключения относительно k_л:

(4.5)

Возвратимся к исходной нелинейной системе. Будем рассматривать нелинейный элемент как будто бы линейный, но имеющий следующее отличие от действительно линейного. В то время, как линейный элемент имеет коэффициент усиления

,

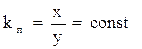у нелинейного элемента отношение выходной величины ко входной («коэффициент усиления нелинейного элемента» k_н) не постоянно и является функцией входной величины:

.

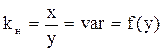Для рассматриваемой нами нелинейной характеристики эта функция имеет вид (рис.4.8):

Рис.4.8. Зависимость k_н от входной величины нелинейного

элемента типа «ограничение по мощности».

При таком подходе устойчивость либо неустойчивость САР определяется условиями

(4.6)

При больших начальных отклонениях у коэффициент k_н мал, и система обладает свойством устойчивости, то есть колебания величины у стремятся затухнуть. О таком свойстве нелинейной системы говорят, что система «устойчива в большом». При малых начальных отклонениях у коэффициент k_н велик, система не обладает свойством устойчивости, и колебания нарастают. Система «неустойчива в малом». Однако это одна и та же система, поэтому независимо от величины начального отклонения у в системе самопроизвольно установятся незатухающие колебания, соответствующие некоторому критическому значению k_н (рис.4.9),которые по причине самовозникновения названы автоколебаниями. Будучи некоторым аналогом границы устойчивости линейных систем, автоколебания, однако, существенно отличаются от границы устойчивости линейных систем. Пусть, например, характеристическое уравнение линейной САР имеет вид

р³ + Ар² + Вр + 1=0.

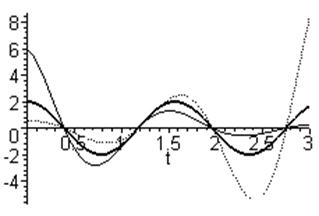
Рис.4.9. Автоколебания.

k_н мало;

k_н велико;

критическое значение k_н.

Система находится на границе устойчивости при условии

А>0; В>0; АВ=1.

При любом сколь угодно малом изменении коэффициентов А или В система уйдёт с границы устойчивости, став либо устойчивой (АВ>1), либо неустойчивой (АВ<1). В нелинейной же системе при изменении каких-либо параметров она не обязательно уйдёт с границы устойчивости. В ней может установиться режим новых автоколебаний, соответствующий новому критическому значению k_н, при котором изменятся параметры колебаний (амплитуда, частота, фаза). Система как бы «сама» подбирает новое значение k_н.

4.4. Приближенное решение задачи об автоколебаниях. Метод

гармонического баланса Крылова-Боголюбова.

Имеется много методов решения такой задачи. Метод Крылова-Боголюбова является одним из наиболее употребительных. Идея метода заключается в желании применить для исследования хорошо развитый аппарат линейной теории автоматического регулирования. Решается задача установления факта существования либо отсутствия автоколебаний, и для случая их существования определяются их параметры. Для этих целей находится математическое описание такого линейного элемента, который, будучи введён в систему вместо нелинейного, обеспечит системе эквивалентные свойства в смысле факта наличия или отсутствия незатухающих колебаний, и только в этом смысле. В переходных процессах эквивалентность поведения исходной нелинейной и заменяющей её линейной систем никак не гарантируется. Процедура такой замены называется гармонической линеаризацией нелинейной характеристики, и она является первым этапом решения задачи.

Постановка задачи. Система представляется в виде совокупности линейной части с передаточной функцией W_л и нелинейного элемента, осуществляющего преобразование x=F(y) (рис.4.10).

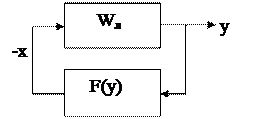
Рис.4.10. Исходная нелинейная САР.

Гармоническая линеаризация нелинейной характеристики.

Примем допущение о том, что на входе нелинейного элемента величина у изменяется по гармоническому закону

,

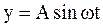корректность которого обсудим в дальнейшем. Определим производную

y΄= py = Aωcosωt.

Приняв обозначение

,

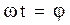получим

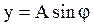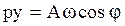; . (4.7)

При такой форме входного сигнала на выходе нелинейного элемента величина х будет изменяться пусть не по гармоническому, но, во всяком случае, по периодическому закону. В этом случае она может быть представлена в виде ряда Фурье

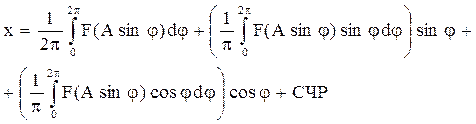(4.8)

Учтя на основании (4.7), что

; ,

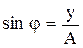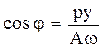преобразуем (4.8):

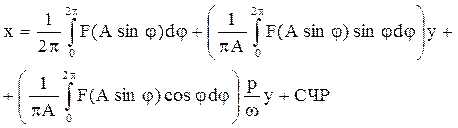
(4.9)

В режиме установившихся колебаний, когда

A=const.; w=const.

первый член ряда – постоянная величина, характеризующая смещение центра колебаний, и в интересующем нас вопросе (есть автоколебания или нет) может быть игнорирована. СЧР – старшие члены ряда, содержащие высшие гармоники, амплитуды которых обычно пренебрежимо малы по сравнению с амплитудой первой гармоники, и потому также могут быть игнорированы. Тогда колебания на выходе нелинейного элемента приближённо представляются в виде

(4.10)

При постоянных А и w выражения в скобках уравнения (4.10) – постоянные величины, и приняв обозначения

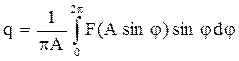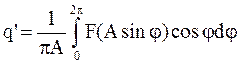; , (4.11)

получим уравнение линейного элемента, эквивалентного по поведению исходному нелинейному в смысле факта существования или отсутствия незатухающих колебаний (напомним, что р представляет собою оператор дифференцирования ):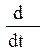

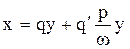. (4.12)

Коэффициенты этого уравнения q и q΄ называются коэффициентами гармонической линеаризации, они являются функциями параметров нелинейных характеристик и обладают следующими свойствами.

1.Для однозначных нелинейных характеристик q΄= 0, поскольку

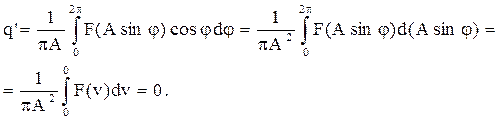
2.Для однозначных нелинейных характеристик

.

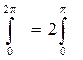3.Для симметричных однозначных нелинейных характеристик

.

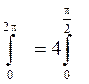Рассмотрим пример расчёта коэффициентов гармонической линеаризации для нелинейной характеристики релейного типа с параметрами е и с, показанными на рис(4.11).

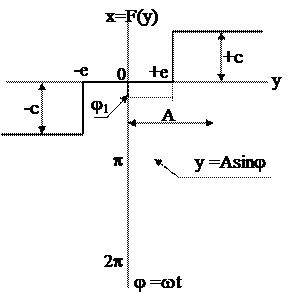Рис.4.11. Релейная нелинейность.

y < -e Þ F(y) = -c;

-e £ y £ +e Þ F(y) = 0;

y > +e Þ F(y) = +c.

1.Поскольку нелинейная характеристика однозначна, то q΄=0.

2.

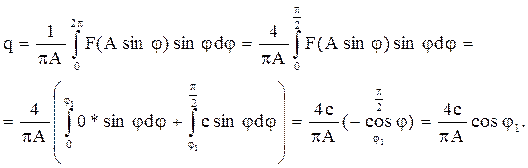
Поскольку , ,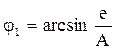

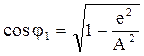и окончательно

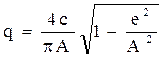. (4.13)

В литературе по теории автоматического регулирования приводятся заранее рассчитанные значения коэффициентов гармонической линеаризации для разнообразных нелинейных характеристик в функциях параметров нелинейных характеристик.

Определение параметров автоколебаний.

Полученные в результате гармонической линеаризации значения коэффициентов q и q΄подставляются в характеристическое уравнение (в данном примере это уравнение (4.3):

.

Используем условие границы устойчивости (4.6):

. (4.14)

Отсюда определяется амплитуда А. Если полученное значение А окажется положительным числом, то в системе присутствуют автоколебания именно с такой амплитудой. В нашем конкретном случае при обозначении

,

,

.

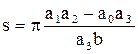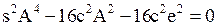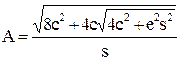Частоту автоколебаний для данного конкретного случая можно определить, выполнив в характеристическом уравнении подстановку p=iw:

,

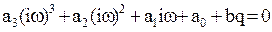откуда, воспользовавшись мнимой частью комплексного числа, получаем

,

то есть в данном конкретном случае частота автоколебаний не зависит от параметров нелинейной характеристики, а определяется только свойствами линейной части системы.

Примечание.

О допустимости пренебрежения старшими членами ряда Фурье.

Величина х содержит сумму гармоник, поступающую на вход линейной части системы. Последняя, как было отмечено при рассмотрении амплитудно-частотных характеристик, является фильтром низких частот, то есть подавляет высокочастотные составляющие. Обычно свойства линейной части системы таковы, что амплитуда уже второй гармоники намного меньше амплитуды первой. Во всяком случае, легко проанализировать АЧХ линейной части, и если амплитуда второй гармоники хотя бы в пять раз меньше, чем второй, то применимость метода не вызывает сомнений.

4.5. Об устойчивости нелинейных систем.

Очевидно, что существенно нелинейные системы требуют индивидуального подхода при оценке их устойчивости. Для нелинейных систем, не относящихся к существенно нелинейным, а содержащим нелинейные характеристики, допускающие их представление рядами Тейлора, возможно сделать выводы об устойчивости на основании анализа устойчивости их линеаризованных моделей. Это позволяют сделать следующие теоремы А.М. Ляпунова:

1. Реальная нелинейная система, устойчива, если устойчива её линейная модель.

2. Реальная нелинейная система, неустойчива, если неустойчива её линейная модель. При этом никакой учёт старших членов рядов Тейлора не изменит вывода об устойчивости.

3. Если линейная модель системы находится на границе устойчивости, то об устойчивости исходной нелинейной системы ничего нельзя сказать без дополнительных исследований.

5. ЭЛЕМЕНТЫ ТЕОРИИ

ДИСКРЕТНЫХ АВТОМАТИЧЕСКИХ СИСТЕМ

В дискретной системе (либо в некоторой её части) сигнал не непрерывно зависит от времени, а имеет дискретную (прерывистую) форму. В такой системе присутствует элемент, преобразующий непрерывный сигнал в прерывистый. Указанное преобразование называют часто квантованием (дроблением). Различают квантование по уровню, квантование по времени, и комбинированное. Квантование по уровню соответствует появлению сигнала в виде ряда дискретных уровней в произвольные моменты времени (рис.5.1,а). При квантовании по времени обеспечивается фиксация дискретных моментов времени, в которые уровень сигнала может принимать произвольные значения (рис.5.1,б). При третьем виде квантования непрерывный сигнал заменяется дискретными уровнями, ближайшими к значениям непрерывного квантуемого сигнала в дискретные моменты времени (рис.5.1,в).

а б в

Рис.5.1. Квантование непрерывного сигнала.

x₁- непрерывный сигнал,

x₂ - квантованный сигнал.

В результате квантования по уровню непрерывная функция времени x₁(t) заменяется ступенчатой функцией. При квантовании по времени непрерывный сигнал x₁(t) заменяется так называемой решётчатой функцией

x₁(nT), если t = nT, n = 0,1,2,…;

x₂(t) = (5.1)

0, если t ≠ nT,

где T – шаг квантования по времени, или период дискретности.

Важным при этом является тот факт, что ординаты решётчатой функции точно равны значениям непрерывного сигнала в дискретные моменты времени t=nT.

Среди большого разнообразия дискретных элементов в системах автоматики весьма распространены импульсные элементы (ИЭ), осуществляющие квантование воспринимаемого ими сигнала по времени. В дальнейшем будут рассматриваться элементы теории именно импульсных систем автоматического регулирования, в состав которых импульсный элемент входит как обязательная часть, и при этом осуществляется квантование только по времени. Кроме того, здесь мы ограничимся рассмотрением линейных импульсных систем.

В практически использующихся дискретных системах ИЭ обычно располагается в цепи сигнала ошибки, поэтому во многих случаях функциональная схема замкнутой импульсной системы с одним импульсным элементом ИЭ и непрерывной частью НЧ может быть представлена в виде, показанном на рис.67. К дискретным системам относятся также цифровые системы управления, содержащие цифровые управляющие машины (ЦУМ), которые могут выполнять функции задающих, сравнивающих и корректирующих устройств.

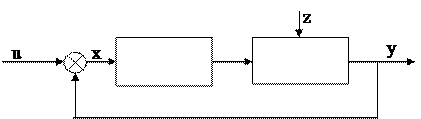ИЭ НЧ

Рис.5.2. Функциональная схема замкнутой

импульсной системы.

Формы импульсов, генерируемых ИЭ, могут быть самыми разнообразными (но одинаковыми для конкретного ИЭ): прямоугольными, треугольными, параболическими и т.п.

В зависимости от того, какой параметр импульса принимается в качестве носителя информации о значении непрерывной величины, употребляют термин «модуляция», сопровождаемый указанием, какая именно модуляция осуществляется импульсным элементом. Существует три основных типа модуляции:

- амплитудно-импульсная (АИМ), при которой информативным признаком является высота импульса, прямо пропорциональная (в частном случае равная) значению непрерывной величины на шаге квантования. Ширина импульса постоянна, а моменты начала импульсов разделены периодом повторения T₀ (рис.5.3,б).

- широтно-импульсная (ШИМ), при которой информативным признаком является ширина импульса, прямо пропорциональная значению непрерывной величины. Высота импульсов постоянна, а моменты начала импульсов разделены периодом повторения T₀ (рис.5.3,в).

- время-импульсная (ВИМ), называемая также фазо-импульсной, при которой сохраняются постоянными высота и ширина импульсов, а носителем информации является момент начала импульса: чем больше значение непрерывной величины, тем позже возникает импульс (рис.5.3,г). Графики рис.5.3 приведены для случая импульсов прямоугольной формы.

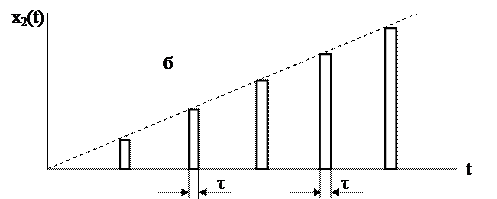Рис.5.3. Типы модуляции.

а– непрерывный сигнал, б – АИМ, в – ШИМ, г – ВИМ.

5.1. Дискретные функции, их разности и суммы.

Для математического описания импульсных систем используют разностные уравнения, а для решения таких уравнений применяют метод прямого и обратного преобразования Лапласа (метод z-преобразования). Как отмечено выше, при этом имеют дело с решётчатыми функциями, которые существуют только при дискретных равноотстоящих друг от друга значениях времени, а между этими значениями функции равны нулю (рис.5.4).

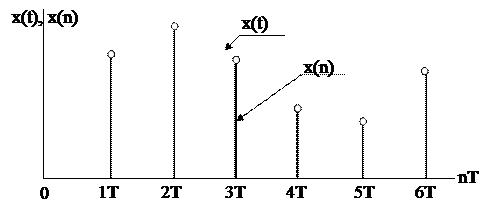Рис.5.4. Решётчатая функция.

Очевидно, что решётчатая функция однозначно определяется видом непрерывной функции и моментами дискретности, но обратное несправедливо, поскольку одна и та же решётчатая функция может быть образована различными непрерывными функциями. Решётчатую функцию обозначают обычно x[nT] либо f[nT], где Т–шаг квантования, а n –целое число (n=0, 1, 2 …). Если расстояние между соседними значениями дискретной функции положить равным единице, то можно перейти к нормированному времени и решётчатую функцию обозначать сокращённо через x[n] или f[n]. Значения этой функции соответствуют ординатам функции с номерами 0, 1, 2,…, n-1, n… Таким образом, можно обозначить:

x[n] = {x₀, x₁,x₂, …,x_n};

f[n] = {f₀, f₁, f₂, …,f_n}. (5.2)

Например, для единичной функции x[n] = 1[n]

x[n] = {1, 1, 1, …, 1}.

Для линейной функции x[n] = n

x[n] = {0, 1, 2, …, n}.

Для экспоненциальной функции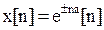

.

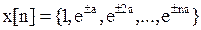Аналогами производных для дискретных нормированных функций являются разности. Так, аналогом первой производной, характеризующей скорость изменения дискретной функции, является разность первого порядка, или первая разность, определяемая выражением

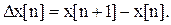(5.3)

Разность второго порядка, или вторая разность,

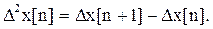(5.4)

Соответственно разность порядка m определена как

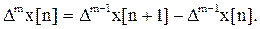(5.5)

На основании применения метода полной математической индукции m-я разность выражается формулой

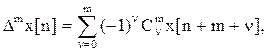(5.6)

где 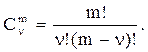- биномиальный коэффициент.

По аналогии с разностями определяются суммы, которые могут рассматриваться как аналоги интегралов. Сумма X_n (n=1, 2, 3, …) равна

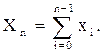(5.7)

5.2. Уравнения в конечных разностях.

Соотношение между решётчатой функцией и её разностями определяет уравнение в конечных разностях, или разностное уравнение. Линейное разностное уравнение можно представить в виде

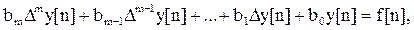(5.8)

где f[n] – заданная функция, y[n] – искомая функция.

Если в уравнении (5.8) заменить разности решётчатой функции их значениями в соответствии с соотношением (5.6), то разностное уравнение запишется в виде

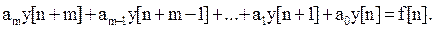(5.9)

Коэффициенты a_i и b_i уравнений (5.8) и (5.9) связаны следующими соотношениями:

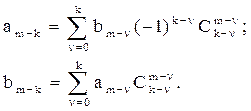(5.10)

Аналогично дифференциальным уравнениям в зависимости от того, равна либо не равна нулю правая часть разностного уравнения, оно называется однородным либо неоднородным. Разностное уравнение, содержащее y[n] и y[n+m], называется уравнением порядка m. Например, уравнение (5.9) при a_m≠ 0 и a₀ ≠ 0 является неоднородным разностным уравнением порядка m.

Для решения уравнения (5.8), то есть для нахождения значений искомой дискретной функции в отдельные моменты времени, должна быть задана функция f[n], а также должны быть известны начальные условия, то есть начальные значения искомой функции и всех её разностей до (m-1)-й включительно.

Методы решения разностных и дифференциальных уравнений сходны. При решении разностных уравнений может быть применён классический метод решения, когда используется подстановка в разностное уравнение предполагаемого решения

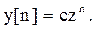
В результате такой подстановки получается характеристическое уравнение, зная корни которого, составляют общее решение. Постоянные суммирования c_i, входящие в общее решение (их количество равно порядку разностного уравнения m), определяются через значения функции в первые m циклов.

В инженерной практике для решения разностных уравнений широко применяется операторный метод, основанный на использовании дискретного преобразования Лапласа и позволяющий значительно упростить решение.

5.3. Дискретное преобразование Лапласа и z-преобразование.

Дискретное преобразование Лапласа является функциональным преобразованием решётчатых функций f[n] и определяется соотношением

(5.11)

В этом выражении q = σ+iω – комплексное число, называемое параметром преобразования. Функцию f[n] называют оригиналом, а F(q)- изображением. Чтобы изображение F(q) было определено, необходима сходимость ряда (5.11). Доказано, что если ряд (5.11) сходится при Re(q)=σ₀, то он сходится при любых q, удовлетворяющих условию Re(q) >σ₀. Значение σ_с, для которого при σ ≥ σ_с ряд сходится, а при σ < σ_с расходится, называется абсциссой сходимости. Ряд сходится, если σ_с < ∞, в противном случае он расходится, и изображение для f[n] не существует.

Положив 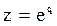, приходим к так называемому z-преобразованию функции f[n], определяемому как

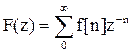. (5.12)

В табл.2 приведены z-преобразования некоторых функций.

Табл.2

1[n]

n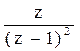

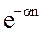
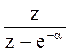
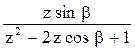
Изображения решётчатых функций являются функциями комплексного переменного e^q, которое может быть записано в виде

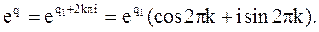(5.13)

Из этого следует, что e^q – периодическая функция вдоль мнимой оси комплексного переменного с периодом 2π. Следовательно, изображения являются периодическими функциями вдоль мнимой оси.

Прямое преобразование Лапласа решает задачу нахождения изображения по оригиналу. Обратная задача, то есть нахождение оригинала по изображению, решается в соответствии с формулой

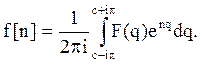(5.14)

В литературе имеются таблицы соответствия между оригиналами и изображениями различных конкретных решётчатых функций.

5.4. Передаточные функции дискретных систем.

Если дискретная система имеет входную величину x(t) и выходную y(t),то передаточной функцией этой системы является

W(z) = Y(z)/X(z), (5.15)

где Y(z) и X(z) – изображения функций времени y[n] и x[n]. Очевидно, что если система находится под действием возмущающего и управляющего воздействий, то z-преобразование выходной величины находится как сумма произведений z-преобразований возмущающего и управляющего воздействий на передаточные функции по соответствующим входам.

Отметим, что знаменатель передаточной функции ДАС, как и для непрерывных систем, называется характеристическим полиномом. Вообще же действия над передаточными функциями дискретных систем аналогичны таковым в отношении непрерывных систем.

5.5. Устойчивость дискретных систем.

Формулировка понятия устойчивости является общей независимо от того, непрерывна система или дискретна. Реакция линейной ДАС на входной сигнал так же, как и непрерывной системы, есть сумма переходной и установившейся составляющих:

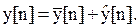(5.16)

Значения выходной величины ДАС, соответствующие моментам времени t = n T, могут быть найдены по выражению

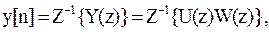(5.17)

где под U(z) понимается z-преобразование любого из входных сигналов, поступающих на ДАС, а Z^-1 означает обратное z-преобразование (имеются соответствующие таблицы).

Аналогично рассуждениям, проведенным при рассмотрении устойчивости непрерывных систем, можно утверждать, что для ДАС устойчивость имеет место при выполнении условия

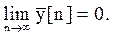(5.18)

Оценка устойчивости импульсной системы может быть выполнена различными способами. Аналогично непрерывным системам можно исследовать либо разностные уравнения, либо частотные характеристики.

Если переходный процесс в импульсной системе описывается разностным уравнением m-го порядка

a_mу[n+m]+a_m-1y[n+m-1]+ … +a₁y[n+1]+a₀y[n]=0, (5.19)

то общее решение имеет вид

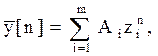(5.20)

где A_i – постоянные коэффициенты, определяемые из начальных условий, z_i – корни характеристического уравнения

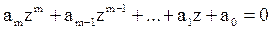. (5.21)

Из (5.21) следует, что для устойчивости, то есть для выполнения условия (5.18), необходимо и достаточно, чтобы все корни уравнения (5.21) были по модулю меньше единицы:

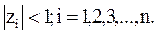
Это означает, что для устойчивости необходимо, чтобы все корни характеристического полинома были расположены внутри круга единичного радиуса с центром в начале координат плоскости z (рис.5.5).

Очевидно, что возникает необходимость в нахождении корней характеристического уравнения.

Аналог критерия Гурвица. Характеристическое уравнение (5.21) преобразуется подстановкой

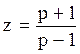, (5.22)

в результате чего оно приводится к виду

b_mp^m + b_m-1p^m-1 + … + b₁p + b₀ =0. (5.23)

Подстановка (5.22) преобразует площадь внутри единичного круга плоскости z в левую полуплоскость p (рис.5.5), после чего, применяя к (5.23) критерий Гурвица, можно судить об устойчивости системы импульсного регулирования.

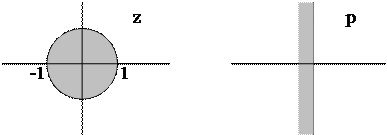Рис.5.5.Круг единичного радиуса плоскости комплексного

переменного z и плоскость комплексного переменного p.

Поскольку ДАС вследствие наличия импульсного элемента реагирует не на сигнал y(t), а на сигнал y[nT], то условие устойчивости (5.18) эквивалентно тому, что стремится к нулю функция, проходящая через точки, соответствующие моментам времени t = nT, и это ещё не означает, что функция y(t) также затухает. Возможны случаи «скрытой» неустойчивости, когда несмотря на затухающий характер функции y[n] характер функции y(t) является расходящимся (рис.5.6).

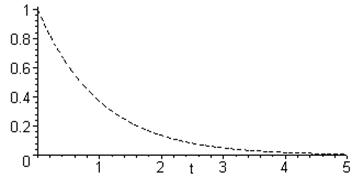
Рис.5.6. Проявление «скрытой» неустойчивости.

Отметим, что для импульсных систем имеются также критерии устойчивости – аналоги критериев Михайлова и Найквиста непрерывных систем.

В отношении показателей качества процессов регулирования дискретных систем соображения аналогичны таковым для непрерывных систем.

6. СОВРЕМЕННЫЕ СРЕДСТВА РЕШЕНИЯ ЗАДАЧ

ТЕОРИИ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ

Развитие компьютерной техники сделало возможным эффективно применять известные уже более полутора-одного столетия математические методы численного решения систем дифференциальных уравнений. При этом достигается точность вычислений, во многих случаях превосходящая необходимую. Вполне удобной является организация ввода данных и интерпретация результатов. Среди средств, которые удобно применить именно к задачам теории автоматического регулирования, относятся следующие.

1.Среда программирования HP VEE for Windows (Hewlett-Packard Visual Engineering Environment) и её развитие – среда VEE PRO. Они отличаются широким математическим обеспечением, расширенными сервисными возможностями и позволяют пользователю конструировать программы путём соединения между собою типовых пиктограмм из фондов системной библиотеки и представлять данные в естественной для инженерного и научного исследования форме. На рис.6.1 приведен пример модели для решения задачи анализа системы «обьект-ПИД-регулятор».

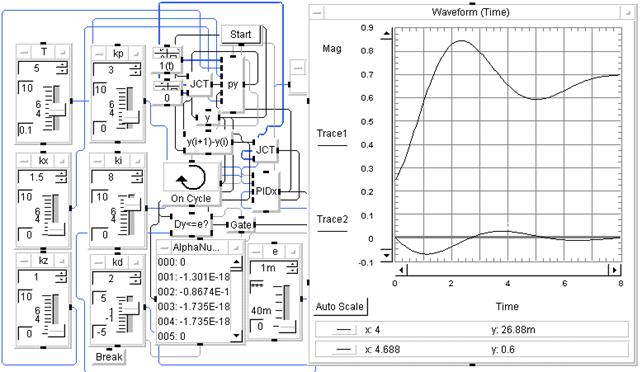
Рис.6.1. Модель «объект - ПИД-регулятор» в среде HP VEE.

При работе в этой среде возникают некоторые затруднения, если в задаче рассматривается система с обратными связями, которые, однако, преодолеваются по приобретении некоторого опыта.

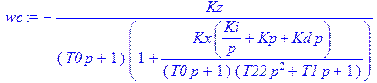
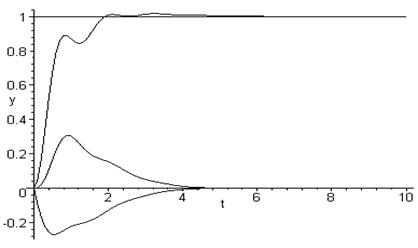
2. Пакет математических программ Maple 6 и его развития. Он позволяет производить, помимо многого другого, решение задач в символьной форме (если такие решения возможны), что очень важно, например, при нахождении передаточной функции системы звеньев. Запись программ на языке этого пакета максимально приближена к традиционным математическим выражениям. Очень хорошо оформлена программа помощи пользователю, содержащая множество примеров. Ниже приведена программа решения задачи анализа САР 4 порядка с ПИД-регулятором с промежуточными результатами нахождения передаточной функции САР по возмущению, а на рис.6.2 - результаты решения (графики переходных процессов). Ещё ниже показана программа для некоторой нелинейной системы 3 порядка, а на рис.6.3 – переходные процессы в ней.

САР 4 ПОРЯДКА С ПИД-РЕГУЛЯТОРОМ

Дифференциальные уравнения

ОР (T0p+1)Y=KxX-KzZ

ЧЭ (T22p^2+T1p+1)X1=-Y

ИМ+РО pX=Kp*pX1+KiX1+Kdp^2X1

Передаточные функции

> restart; Wx:=Kx/(T0*p+1):Wz:=-Kz/(T0*p+1):W1:=1/(T22*p^2+T1*p+1):W2:=Ki/p+Kp+Kd*p:Wp:=W1*W2:wc:=Wz/(1+Wx*Wp);s:=simplify(wc):Ws:=collect((s),p);

>

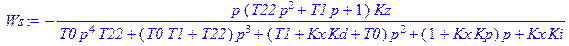
with(plots):T0:=1:Kx:=1:Kz:=1:T22:=0.05:T1:=0.2:Kp:=2.0:Ki:=2:Kd:=0.5: sys:=T0*diff(y(t),t)+y(t)=Kx*x(t)-Kz*1(t), T22*diff(x1(t),t$2)+T1*diff(x1(t),t)+x1(t)=-y(t),diff(x(t),t)=Kp*diff(x1(t),t)+Ki*x1(t)+Kd*diff(x1(t),t$2):fcns:={y(t),x1(t),x(t)}:p:=dsolve({sys,y(0)=0,x1(0)=0,D(x1)(0)=0,x(0)=0},fcns,type=numeric,method=rkf45):odeplot(p, [[t,x(t)],[t,x1(t)],[t,0(t)],[t,y(t)],[t,1(t)]],0..10,thickness=1,numpoints=101,color=black,labels=[t,y]);

>

Рис.6.2. Переходные процессы в САР 4 порядка.

> restart;

> with(plots):a:=0.15:c:=0.5:b:=a+c:T0:=2:T1:=0.2:Tc:=0.25:Kx:=2:Kp:=5:pn:=501:z(t):=0.25(t):e(t):=x1(t)-x(t):f(t):=piecewise(e(t)<-b,-c,e(t)>=-b and e(t)<-a, c*(e(t)+a)/(b-a),e(t)>=-a and e(t)<a,0,e(t)>=a and e(t)<b,c*(e(t)-a)/(b-a),c): sys:=T0*diff(y(t),t)+y(t)=Kx*x(t)-z(t),T1*diff(x1(t),t)+x1(t)=-Kp*y(t),Tc*diff(x(t),t)=f(t):fncs:={y(t),x1(t),x(t)}: p:=dsolve({sys,y(0)=0,x1(0)=0,x(0)=0},fncs,type=numeric,method=rkf45):odeplot(p,[[t,y(t)],[t,x1(t)],[t,z(t)],[t,x(t)],[t,e(t)],[t,f(t)]],0..10,numpoints=pn,labels=[t,"y,x1,z,x,(x1-x),f"],thickness=2,title=`red=y, green=x1, yellow=z, blue=x, magenta=(x1-x), aquamarine=f`);

Warning, the name changecoords has been redefined

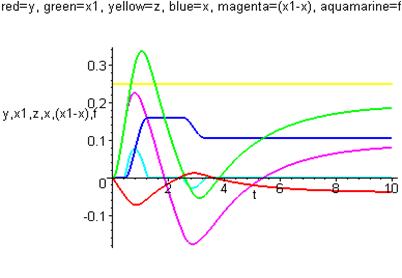
Рис.6.3. Переходные процессы в нелинейной САР.

3. Пакет математических программ MATLAB, начиная с 6 версии. Чрезвычайно мощное средство решения огромного круга задач. Содержит в своём составе пакет SIMULINK, специализированный для решения задач автоматического регулирования. В пакете SIMULINK имеется обширная библиотека элементов систем автоматики, включающая линейные и нелинейные, непрерывные и дискретные элементы. Решение задачи сводится к построению структурной схемы системы, указанию параметров отдельных элементов, выбору предпочтительного варианта отображения результатов и запуску на расчёт. Пакет содержит меню численных методов решения, допускающее автоматический выбор шага (постоянного либо переменного). Гарантированная относительная погрешность решения составляет 1*10^-14. Имеется развитая структура помощи пользователю. Ёмкость пакета SIMULINK, обладающего самостоятельностью функционирования, без консультационной документации составляет около 200 мегабайт.

На рис.6.4 показана структура, набранная для исследования работы системы регулирования частоты вращения вала главного судового дизеля в условиях волнения моря для двух различных схем включения регулятора: предельной и всережимной.

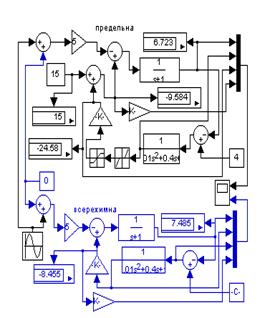
Рис.6.4. Модели САР с регуляторами,

включёнными по различным схемам.

Результаты решения (графики процессов) выводятся в форме, предпочитаемой исследователем, например, аналогично тому, как это выполняется в среде Maple. При этом имеются возможности очень гибкого изменения масштабов в широком диапазоне.

Рекомендуемая литература

1. Бесекерский В.А., Попов Е.В. Теория систем автоматического регулирования. М.: Наука, 1972.- 767 с.

2. Воронов А.А. Основы теории автоматического управления. Ч.1. М.: Энергия, 1965.- 396 с.

3. Воронов А.А. Основы теории автоматического управления. Ч.2. М.: Энергия, 1966.- 384 с.

4. Гитис Э.И., Данилович Г.А., Самойленко В.И. Техническая кибернетика. М.: Советское радио, 1969.- 486 с.

5. Под ред. Пономарёва В.М. и Литвинова А.П. Основы автоматического регулирования и управления. М.: Высшая школа, 1974.- 439 с.

6. Под ред. Солодовникова В.В. Техническая кибернетика. Книга 1.- 768 с., Книга 2.- 679 с., Книга 3, Ч.1.- 607 с.,Ч.2.- 367 с. М.: Машиностроение, 1967 – 1968.

7.Юревич Е.И. Теория автоматического управления. Л.: Энергия, 1975.- 404 с.

СОДЕРЖАНИЕ

ВВЕДЕНИЕ 3

1.ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ 4

1.1. Управление и регулирование 4

1.2. Состав системы автоматического регулирования 5

1.3. Принципы автоматического регулирования 6

1.4. Типовая функциональная схема САР 9

1.5. Классификация САР по характеру изменения

регулируемой величины 10

1.6. Математический аппарат теории автоматического

регулирования 11

1.7. Задачи теории автоматического регулирования 12

1.8. Требования к системам автоматического регулирования 12

1.9. Режимы работы САР 14

1.10. Типовые внешние воздействия 16

2. ПРИМЕРЫ СИСТЕМ АВТОМАТИЧЕСКОГО

РЕГУЛИРОВАНИЯ 16

2.1. Система стабилизации уровня в ёмкости 16

2.2. Регулятор частоты вращения вала главного судового дизеля 17

2.3.Регулятор частоты вращения вала непрямого действия 17

2.4. Регулятор с жёсткой обратной связью 18

2.5. Регулятор с гибкой обратной связью 19

3. ЛИНЕЙНЫЕ АВТОМАТИЧЕСКИЕ СИСТЕМЫ 20

3.1. Объект регулирования 21

3.2. Типовые динамические звенья 27

3.3. Передаточная функция 36

3.4. Вынужденные колебания и частотные характеристики САР 40

3.5. Устойчивость автоматических систем 44

3.6. Качество процессов регулирования 56

3.7. Взаимодействие объекта и регулятора.

Законы регулирования 59

3.8. Противоречие между статической точностью

и устойчивостью 65

4. НЕЛИНЕЙНЫЕ АВТОМАТИЧЕСКИЕ СИСТЕМЫ 66

4.1. Типовые нелинейные характеристики и их

влияние на качество регулирования 67

4.2. Основные отличия нелинейных систем от линейных 69

4.3. Автоколебания в нелинейных системах и

физическая картина их возникновения 70

4.4. Приближённое решение задачи об автоколебаниях. Метод

гармонического баланса Крылова – Боголюбова 73

4.5. Об устойчивости нелинейных систем 78

5. ЭЛЕМЕНТЫ ТЕОРИИ ДИСКРЕТНЫХ СИСТЕМ 79

5.1. Дискретные системы, их разности и суммы 82

5.2. Уравнения в конечных разностях 83

5.3. Дискретное преобразование Лапласа и z-преобразование 84

5.4. Передаточные функции дискретных систем 86

5.5. Устойчивость дискретных систем 86

6. СОВРЕМЕННЫЕ СРЕДСТВА РЕШЕНИЯ ЗАДАЧ

ТЕОРИИ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ 88