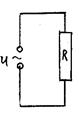
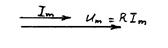
 | Ток через резистор при выполнении условия квазистационарности определяется законом Ома: 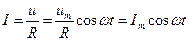 , где , где 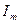 - амплитуда тока, - амплитуда тока, 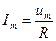 . . |
| Рис. 2. |
Для наглядного изображения соотношений между токами и напряжением воспользуемся методом векторных диаграмм.
 | Диаграмма амплитудных значений тока 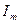 и напряжения и напряжения 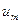 на резисторе. Сдвиг фаз в этом случае между на резисторе. Сдвиг фаз в этом случае между 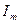 и и 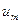 равен 0, равен 0, 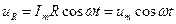 . . |
| Рис.3. |
2. Переменный ток, текущий через катушку индуктивности L
(R = 0, C = 0).
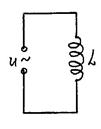 | При протекании по индуктивности переменного тока в ней возникает эдс самоиндукции 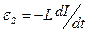 . Закон Ома для неоднородного участка цепи . Закон Ома для неоднородного участка цепи 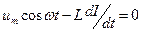 . Откуда . Откуда 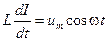 . Так как внешнее напряжение приложено к катушке, то . Так как внешнее напряжение приложено к катушке, то 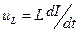 - есть падение напряжения на катушке. - есть падение напряжения на катушке. |
| Рис.4. |
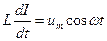
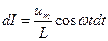
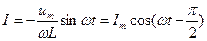
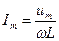
Роль сопротивления играет величина 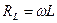 - реактивное индуктивное сопротивление. Если взять
- реактивное индуктивное сопротивление. Если взять 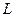 в Генри, а
в Генри, а 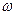 в с-1, то
в с-1, то 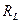 выразится в Омах. Чем больше
выразится в Омах. Чем больше 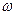 тем больше
тем больше , для постоянного тока
, для постоянного тока 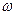 = 0 и поэтому постоянному току индуктивность не оказывает
= 0 и поэтому постоянному току индуктивность не оказывает
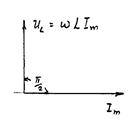 | сопротивления. 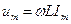 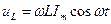 Падение напряжения на индуктивности опережает про фазе ток на Падение напряжения на индуктивности опережает про фазе ток на 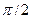 и векторная диаграмма имеет вид рис.5. и векторная диаграмма имеет вид рис.5. |
| Рис. 5. |
3. Переменный ток, текущий через емкость (R = 0, L = 0).
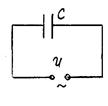 | Когда на емкость подано переменное напряжение, она непрерывно перезаряжается, вследствие чего в цепи течет переменный ток. Напряжение на конденсаторе 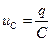 можно считать равным внешнему можно считать равным внешнему 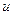 . Тогда . Тогда |
| Рис.6. |
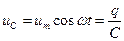
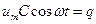
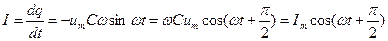 ,
,
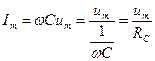 .
.
Величина 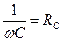 называется реактивным емкостным сопротивлением. Для постоянного
называется реактивным емкостным сопротивлением. Для постоянного
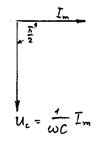 | тока  , то есть постоянный ток через конденсатор течь не может. Падение напряжения на конденсаторе, , то есть постоянный ток через конденсатор течь не может. Падение напряжения на конденсаторе, 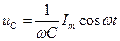 , где , где 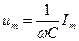 - амплитудное значение напряжения, а ток равен - амплитудное значение напряжения, а ток равен 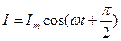 |
| Рис.7. |
Падение напряжения 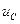 отстает по фазе от текущего через конденсатор тока на
отстает по фазе от текущего через конденсатор тока на 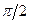 .
.
 2014-02-13
2014-02-13 3974
3974
