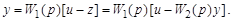
После несложных преобразований получим
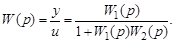 (3.54)
(3.54)
Правило: передаточная функция системы с отрицательной обратной связью равна дроби, в числителе которой стоит передаточная функция прямого канала 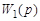 , а знаменатель представляет собой сумму единицы и произведения передаточных функций прямого и обратного каналов системы.
, а знаменатель представляет собой сумму единицы и произведения передаточных функций прямого и обратного каналов системы.
В случае положительной обратной связи формула (3.54) принимает вид
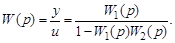 (3.55)
(3.55)
На практике обычно встречаются системы с отрицательной обратной связью, для которых передаточная функция находится по соотношению (3.54).
3.3.4. Правило переноса
В некоторых случаях для получения общей передаточной функции системы с помощью структурных преобразований удобнее было бы перенести точку приложения сигнала через звено ближе к выходу или входу. При таком преобразовании структурной схемы следует придерживаться правила: передаточная функция системы должна оставаться неизменной.
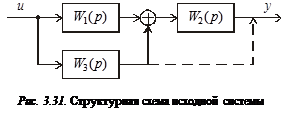
Рассмотрим ситуацию, когда точка приложения сигнала переносится через звено ближе к выходу. Исходная структура системы показана на рис. 3.31. Определим для нее результирующую передаточную функцию
|
|
|
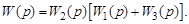 (3.56)
(3.56)
Перенесем точку приложения сигнала через звено с передаточной функцией 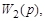 добавив в этот канал некоторую передаточную функцию
добавив в этот канал некоторую передаточную функцию 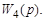 Получим структурную схему преобразованной системы (рис. 3 32).
Получим структурную схему преобразованной системы (рис. 3 32).
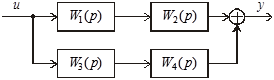 |
Рис. 3.32. Структурная схема преобразованной системы.
Для нее передаточная функция имеет вид
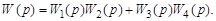 (3.57)
(3.57)
Поскольку при преобразовании структуры системы ее передаточная функция не должна измениться, приравняв правые части выражений (3.56) и (3.57), определим искомую передаточную функцию 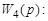
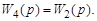 (3.58)
(3.58)
Таким образом, при переносе точки приложения сигнала ближе к выходу системы в канал следует добавить передаточную функцию звена, через которое переносится сигнал.
Аналогичное правило можно сформулировать для переноса точки приложения сигнала ближе к входу системы: в соответствующий канал следует добавить обратную передаточную функцию звена, через которое переносится сигнал.
Пример 3.1
Определить общую передаточную функцию системы, структурная схема которой приведена на рис. 3.33.
Предварительно определим передаточные функции типовых соединений звеньев: передаточная функция параллельного соединения звеньев
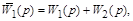
а передаточная функция последовательно соединенных звеньев
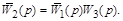
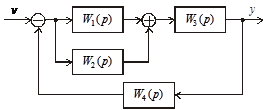 |
Рис. 3.33. Структурная схема системы
С учетом введенных обозначений структуру системы можно привести к виду, изображенному на рис. 3.34.
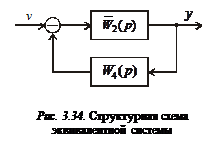 Используя структурные преобразования, запишем общую передаточную функцию системы
Используя структурные преобразования, запишем общую передаточную функцию системы
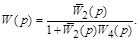
Подставляя вместо 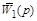 и
и 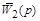 их значения, получим окончательно
их значения, получим окончательно
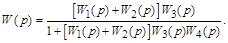
Пример 3.2
Определить передаточную функцию системы автоматического сопровождения цели радиолокационной станции [6], структурная схема которой представлена на рис. 3.35.
|
|
|
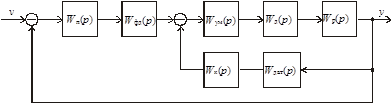
Рис. 3.35. Структурная схема системы автоматического сопровождения цели
Здесь 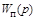 – передаточная функция приемника системы;
– передаточная функция приемника системы; 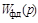 – передаточная функция фазового детектора;
– передаточная функция фазового детектора; 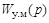 – передаточная функция усилителя мощности;
– передаточная функция усилителя мощности; 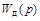 – передаточная функция двигателя;
– передаточная функция двигателя; 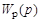 – передаточная функция редуктора;
– передаточная функция редуктора; 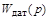 – передаточная функция датчика частоты вращения антенны;
– передаточная функция датчика частоты вращения антенны; 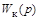 – передаточная функция корректирующего устройства.
– передаточная функция корректирующего устройства.
Используя правила структурных преобразований, запишем
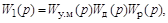
передаточную функцию
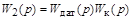
и
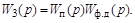
Определим передаточную функцию внутреннего контура
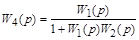
и прямого канала системы
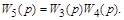
Определим полную передаточную функцию системы
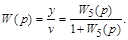
Подставляя вместо промежуточных передаточных функций 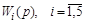 , исходные значения, получим окончательно
, исходные значения, получим окончательно
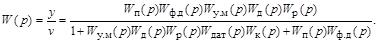
3.4. Структурные схемы, соответствующие дифференциальным уравнениям
Второй способ составления структурной схемы основан на использовании дифференциальных уравнений. Рассмотрим его сначала для объекта, поведение которого описывают векторно-матричные уравнения (2.1), (2.2):
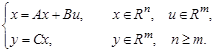 (3.59)
(3.59)
Проинтегрируем уравнение состояния в (3.59) по времени и определим переменные состояния и выхода в виде
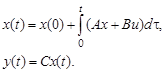 (3.60)
(3.60)
Уравнения (3.60) являются основными для составления схемы.
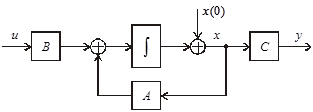 |
Рис. 3.36. Структурная схема, соответствующая уравнениям
состояния объекта
Структурную схему, соответствующую уравнениям (3.60), удобнее изображать, начиная с выходных переменных y, причем входные и выходные переменные объекта желательно располагать на одной горизонтальной прямой (рис. 3.36).
Для одноканального объекта структурную схему можно составить по уравнению (2.3), разрешив его относительно старшей производной
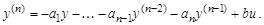 (3.61)
(3.61)
Проинтегрировав (3.61) n раз, получим
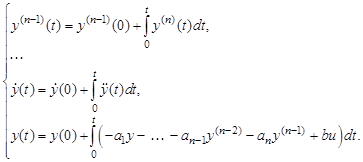 (3.62)
(3.62)
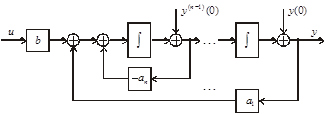
Системе уравнений (3.62) соответствует структурная схема, приведенная на рис. 3.37.
Рис. 3.37. Структурная схема, соответствующая уравнению (3.61)
Как видим, одноканальный объект управления, поведение которого описывает уравнение (3.61), структурно всегда можно представить в виде цепочки из n последовательно соединенных интеграторов с обратными связями.
Пример 3.3
Изобразить структурную схему объекта, модель которого задана следующей системой дифференциальных уравнений:
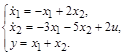
Предварительно проинтегрируем уравнения состояния
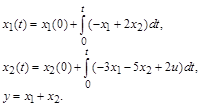
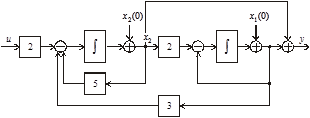 |
Рис. 3.38. Иллюстрация составления структурной схемы
по уравнениям состояния
В соответствии с интегральными уравнениями на рис. 3.38 изобразим структурную схему системы.
3.5. Переход от передаточной функции к каноническому описанию
Обсудим наиболее известные способы преобразования математической модели объекта в виде произвольной передаточной функции к описанию в переменных состояния. Для этой цели используем соответствующие структурные схемы. Отметим, что данная задача неоднозначна, так как переменные состояния для объекта можно выбирать различным образом (см. подразд. 2.2).
Рассмотрим два варианта перехода к описанию в переменных состояния от передаточной функции объекта
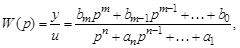 (3.63)
(3.63)
где 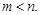 Предварительно представим (3.63) в виде произведения двух передаточных функций:
Предварительно представим (3.63) в виде произведения двух передаточных функций:
1. 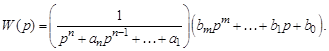 (3.64)
(3.64)
2. 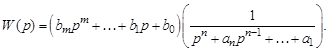 (3.65)
(3.65)
Каждому из этих представлений (3.63) соответствует своя простая модель в переменных состояния, которая называется канонической формой.
3.5.1. Первая каноническая форма
Рассмотрим преобразование математической модели системы с передаточной функцией (3.64). Ее структурную схему можно представить в виде двух последовательно соединенных звеньев
(рис. 3.39).
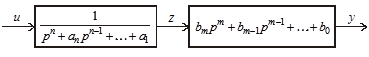
Рис. 3.39. Структурное представление системы (3.64)
Для каждого звена системы запишем соответствующее операторное уравнение
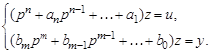 (3.66)
(3.66)
Определим из первого уравнения (3.66) старшую производную переменной z, что соответствует значению 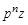 в операторной форме
в операторной форме
|
|
|
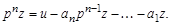
Полученное выражение позволяет представить первое уравнение (3.66) в виде цепочки из n интеграторов с обратными связями (см. подразд. 3.5), а выходная переменная y формируется в соответствии со вторым уравнением (3.66) как сумма переменной z и ее m производных (рис. 3.40).
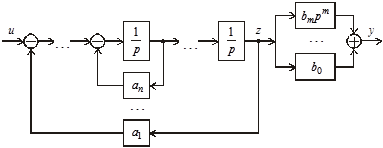
Рис. 3.40. Схема, соответствующая уравнениям (3.66)
Используя структурные преобразования, получим структурную схему системы, приведенную на рис. 3.41.
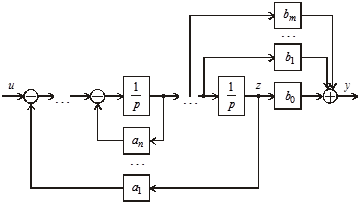
Рис. 3.41. Структурная схема, соответствующая канонической форме
Отметим, что структурная схема, соответствующая передаточной функции (3.64), состоит из цепочки n интеграторов, где n – порядок системы. Причем в обратной связи находятся коэффициенты знаменателя исходной передаточной функции (коэффициенты характеристического полинома), а в прямой связи – коэффициенты полинома ее числителя.
От полученной структурной схемы нетрудно перейти к модели системы в переменных состояния. С этой целью выход каждого интегратора примем за переменную состояния
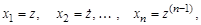
что позволяет записать дифференциальные уравнения состояния и уравнение выхода системы (3.63) в виде
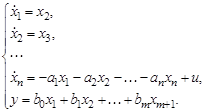 (3.67)
(3.67)
Систему уравнений (3.67) можно представить в векторно-матричной форме (2.1) со следующими матрицами:
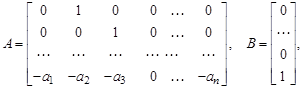
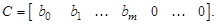
Модель системы в переменных состояния (3.67) будем называть первой канонической формой.
3.5.2. Вторая каноническая форма
Рассмотрим второй способ перехода от передаточной функции (3.63) к описанию в переменных состояния, для чего структуру системы (3.65) схематично представим на рис. 3.42.
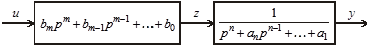 |
Рис. 3.42. Структурное представление передаточной функции (3.65)
Ее операторные уравнения имеют вид
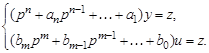 (3.68)
(3.68)
Аналогично предыдущему случаю представим первое уравнение (3.68) в виде цепочки из n интеграторов с обратными связями, а входное воздействие z сформируем в соответствии со вторым уравнением (3.68) в виде суммы управления u и m его производных (рис. 3.43).
В результате структурных преобразований получим структурную схему системы, приведенную на рис. 3.44. Как видим, и в этом случае структурная схема, соответствующая передаточной функции (3.65), состоит из цепочки n интеграторов. В обратной связи также располагаются коэффициенты характеристического полинома, а в прямой связи – коэффициенты полинома ее числителя.
|
|
|
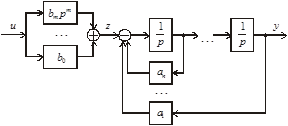
Рис. 3.43. Схема, соответствующая уравнениям (3.68)
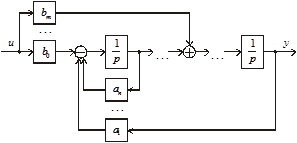
Рис. 3.44. Структурная схема, соответствующая передаточной функции (3.65)
Снова в качестве переменных состояния выберем выходные величины интеграторов и запишем относительно них дифференциальные уравнения состояния и уравнение выхода
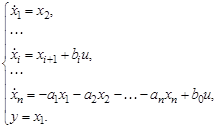 (3.69)
(3.69)
По уравнениям (3.69) определим матрицы
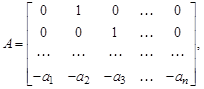
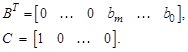
Модель системы в переменных состояния типа (3.69) будем называть второй канонической формой.
Отметим, что матрица A неизменна для первой или второй канонических форм и содержит коэффициенты знаменателя исходной передаточной функции (3.63). Коэффициенты числителя передаточной функции (3.63) содержат матрица C (в случае первой канонической формы) или матрица B (в случае второй канонической формы). Поэтому уравнения состояния, соответствующие двум каноническим представлениям системы, могут быть записаны непосредственно по передаточной функции (3.63) без перехода к структурным схемам, приведенным на рис. 3.40 и 3.43.
Как видим, переход от передаточной функции к описанию в переменных состояния является задачей неоднозначной. Мы рассмотрели варианты перехода к каноническому описанию, которые чаще других используются в теории автоматического управления.
Пример 3.4
Получить два варианта канонического описания и соответствующих структурных схем для системы, модель которой имеет вид
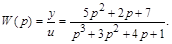
Используем представление передаточной функции в виде (3.64) и запишем для нее операторные уравнения
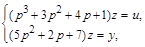
от которых перейдем к структурной схеме, приведенной на рис. 3.45.
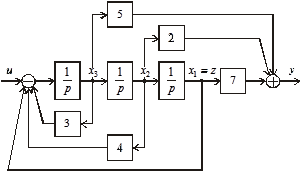
Рис. 3.45. Структурная схема, соответствующая первой канонической форме
На основании этой структурной схемы запишем уравнения первой канонической формы в виде
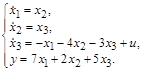
Для перехода ко второй канонической форме представим передаточную функцию системы в виде (3.65) и запишем для нее следующие операторные уравнения:
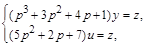
которым соответствует структурная схема, приведенная на рис. 3.46.
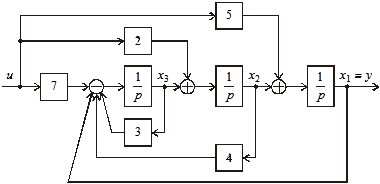
Рис. 3.46. Структурная схема, соответствующая второй канонической форме
Запишем теперь модель системы в виде второй канонической формы
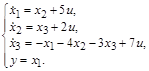
3.6. Область применения структурного метода
Структурный метод удобен при расчете линейных автоматических систем, но имеет свои ограничения. Метод предполагает использование передаточных функций, поэтому может применяться, как правило, при нулевых начальных условиях.
При использовании структурного метода необходимо придерживаться следующего правила: при любом преобразовании системы ее порядок не должен уменьшаться, т. е. недопустимо сокращение одинаковых множителей в числителе и знаменателе передаточной функции. Сокращая одинаковые множители, мы тем самым выбрасываем из системы реально существующие звенья. Проиллюстрируем это утверждение примером.
Пример 3.5
Рассмотрим систему, состоящую из интегрирующего и дифференцирующего звеньев, которые соединены последовательно.
 Первый вариант соединения звеньев показан на рис. 3.47.
Первый вариант соединения звеньев показан на рис. 3.47.
Используя структурные преобразования, найдем общую передаточную функцию
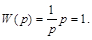
Отсюда следует вывод, что подобное соединение звеньев эквивалентно безынерционному звену, т. е. сигнал на выходе системы повторяет сигнал на ее входе. Покажем это, рассматривая уравнения отдельных звеньев. Выходной сигнал интегрирующего звена определяется соотношением
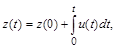
где 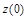 – начальное условие на интеграторе. Сигнал на выходе дифференцирующего звена, а следовательно, и всей системы имеет вид
– начальное условие на интеграторе. Сигнал на выходе дифференцирующего звена, а следовательно, и всей системы имеет вид
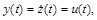
что соответствует выводу, сделанному на основе анализа общей передаточной функции звеньев.
 Второй вариант соединения звеньев показан на рис. 3.48, т. е. звенья поменяли местами. Передаточная функция системы та же, что и в первом случае,
Второй вариант соединения звеньев показан на рис. 3.48, т. е. звенья поменяли местами. Передаточная функция системы та же, что и в первом случае,
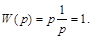
Однако теперь выход системы не повторяет входной сигнал. В этом можно убедиться, рассматривая уравнения звеньев. Сигнал на выходе дифференцирующего звена соответствует уравнению
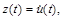
а на выходе системы определяется соотношением
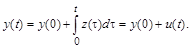
Как видим, во втором случае выходной сигнал отличается от сигнала на выходе первой системы на величину начального значения, несмотря на то, что обе системы имеют одну и ту же передаточную функцию.
Заключение
В этом разделе рассмотрены динамические характеристики типовых звеньев, из которых состоят системы управления произвольной конфигурации. Обсуждены особенности структурных схем, построенных на основе передаточных функций и дифференциальных уравнений. Приведены два способа перехода от передаточной функции системы через структурные схемы к ее моделям в виде переменных состояния, соответствующие различным каноническим формам.
Следует отметить, что представление системы в виде структурной схемы позволяет в ряде случаев оценить ее статику и динамику и дает, по существу, структурный портрет системы.
Задачи
3.1. Изобразить структурную схему системы, дифференциальное уравнение которой имеет вид:
а) 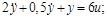
б) 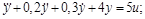
в) 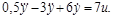
3.2. Изобразить структурную схему системы, модель которой представлена в переменных состояния:
а) 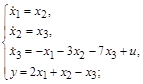 б)
б) 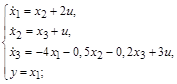
в) 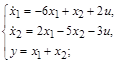 г)
г) 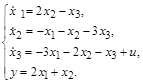
3.3. Определить передаточные функции систем, если их структурные схемы имеют вид, представленный на рис. 3.49.
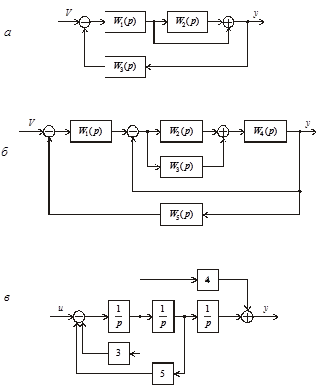
Рис. 3.49. Структурные схемы к задаче 3.3
| |
3.4. Известны структурные схемы системы (рис. 3.50). Записать их модели в переменных состояния.
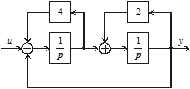
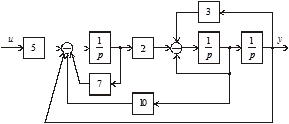
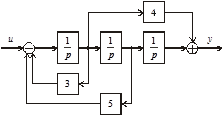
Рис. 3.50. Структурные схемы к задаче 3.4
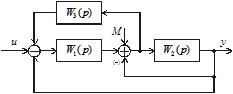
3.5. Известна структурная схема системы (рис. 3.51).
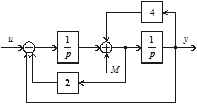
Рис. 3.51. Структурная схема к задаче 3.5
1. Определить передаточную функцию 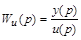 в предполо-жении, что
в предполо-жении, что 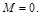
2. Определить передаточную функцию 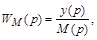 полагая
полагая 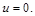
3. Записать модель системы в переменных состояния.
 |
4. Повторить пп. 1 и 2 для системы, структурная схема которой приведена на рис. 3.52.
Рис. 3.52. Структурная схема к задаче 3.5
3.6. Изобразить структурную схему, соответствующую первой канонической форме описания системы, имеющей передаточную функцию
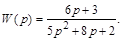
1. Записать первую каноническую форму.
2. Изобразить структурную схему, соответствующую второй канонической форме описания системы.
3. Записать вторую каноническую форму.
3.7. Изобразить структурную схему, соответствующую первой канонической форме описания системы, имеющей передаточную функцию
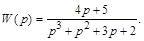
1. Записать первую каноническую форму.
2. Изобразить структурную схему, соответствующую второй канонической форме описания системы.
3. Записать вторую каноническую форму.
3.8. Изобразить структурную схему, соответствующую первой канонической форме описания системы, имеющей передаточную функцию
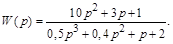
1. Записать первую каноническую форму.
2. Изобразить структурную схему, соответствующую второй канонической форме описания системы.
3. Записать вторую каноническую форму.
Литература
1. Андреев Ю.Н. Управление конечномерными линейными объектами. – М.: Наука, 1978.
2. Бесекерский В.А., Попов Е.П. Теория автоматического регулирования. – М.: Наука, 1974.
3. Ерофеев А. А. Теория автоматического управления. – СПб.: Поли-техника, 1998.
4. Иващенко Н.Н. Автоматическое регулирование. – М.: Машино-строение, 1978.
5. Первозванский А.А. Курс теории автоматического управления. – М.: Высш. шк., 1986.
6. Попов Е.П. Теория линейных систем автоматического регулирования и управления. – М.: Высш. шк., 1989.
7. Коновалов Г.Ф. Радиоавтоматика. – М.: Высш. шк., 1990.
8. Филипс Ч., Харбор Р. Системы управления с обратной связью. – М.: Лаборатория базовых знаний, 2001.
 2015-05-13
2015-05-13 27398
27398
