2014-02-13
365
КИНЕМАТИКА ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ
Механика – изучает движение тел в пространстве с течением времени.
Движение без учета сил действующих на тело, рассматривается в кинематике, а с учетом их в динамике.
В кинематике тела размерами которых можно пренебречь в условиях данной задачи, представляются в виде материальных точек (м.т) являющихся их моделью.Положение м.т. в пространстве определяется с помощью системы координат X,Y,Z, связанной с неподвижным телом (телом отсчета)
Совокупность тела отсчета, жестко связанной с ним системы координат и часов, называется системой отсчета.
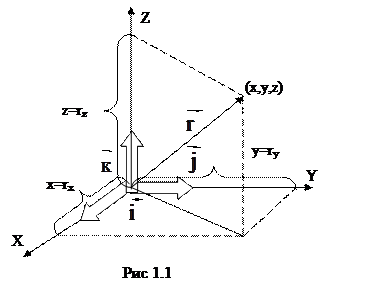Положение материальной точки в декартовой системе координат задается ее координатами x, y, z или радиус-вектором 
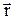, проведенный в заданную точку из начала координат (рис 1.1). Радиус-вектор 
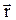и его проекции на оси координат определяются из соотношений:
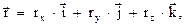
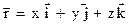, (1.1)
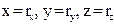где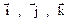 
–
единичные векторы осей координат.
Модуль вектора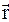 
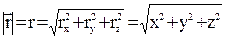(1.2)
При движении м.т. относительно выбранной системы отсчета ее радиус-вектор и его координаты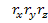
зависят от времени.
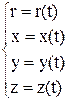(1.3)
Траектория движения м.т в пространстве определяется совокупностью всех ее последовательных положений в пространстве. Уравнение траектории z=z (x,y) находится в результате решения системы уравнений (1.3 ) путем исключения параметраt.
Движение называется прямолинейным, если его траектория – прямая линия, и криволинейным во всех других случаях. Вид траектории не зависит от выбора системы отсчета. При движении м.т. по криволинейной траектории в выбранной системе отсчета, за интервал времени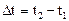 
радиус-вектор изменяется на величину 
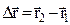, а точка проходит пусть s.
Путь может быть больше модуля вектора перемещения или равен ему. Равенство наблюдается только в частных случаях – при прямолинейном движении тела в одном направлении, и для бесконечно малых промежутков времени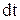 
.
Для характеристики движения м.т. вводят понятие средней и мгновенной скорости.
Средней скоростью называется вектор, равный отношению вектора перемещения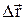 
к промежутку времени 
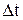, в течение которого произошло перемещение м.т.
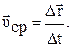
Направление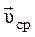 
, совпадает с направлением вектора перемещения , (
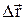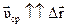) (рис 1.2)
Мгновенной скоростью называется предельное значение вектора средней скорости при стремлении 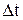к нулю
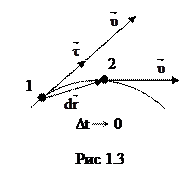
(1.4)
Вектор перемещения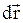 
и скорость 
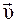направлены по секущей и при стремлении 
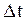к нулю образуют к касательную в точке 1 (рис. 1.3).
Модульмгновенной скорости путевая скорость определяется из соотношения
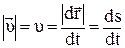, (1.5)
где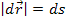 
- путь пройденный точкой за интервал времени dt
Путь, пройденный материальной точкой за интервал времени от t1 до t2
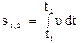(1.6)
С учетом соотношений (1.1)
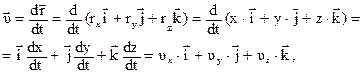(1.7)
где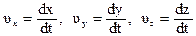 
– проекции скорости точки на оси координат.
Модуль вектора скорости в декартовой системе координат
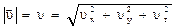(1.8)
В процессе движения направление и модуль вектора скорости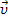 
м.т. могут изменяться. Изменение скорости 
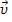определяется векторам ускорения 
.
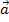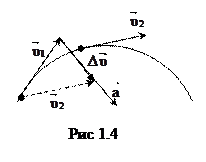
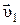, а в момент t2 – скорость 
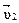(рис. 1.4). Тогда за промежуток времени 
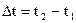вектор скорости изменится на величину 
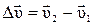, а среднее ускорение
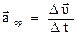(1.9)
Вектор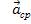
, совпадает с вектором 
.
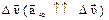Мгновенное ускорение
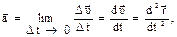(1.10)
где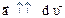 
(рис. 1.4)
С учетом соотношений (1.1) и (1.7)
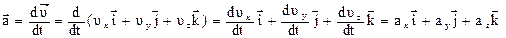(1.11)
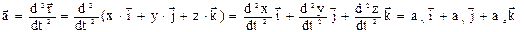
где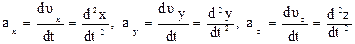
– проекции ускорения точки на оси координат.
