Вращательное движение

Кинематика вращательного и колебательного движения

Лекция 2

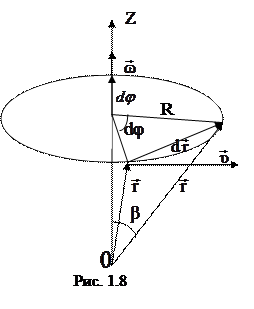Рассмотрим движение м.т. по окружности радиусом R с постоянной линейной скоростью 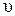вокруг неподвижной оси Z (рис. 1.8).

Положение точки определяется радиус-вектором 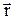, проведенным из начала координат. За малый интервал времени 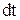радиус-вектор 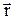повернется на угол 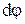. Направление поворота м.т. вокруг оси Z задается вектором 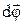, который определяется правилом правого винта: поступательное движение правого винта и вектора 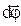совпадают, если вращение точки и винта совершается в одинаковом направлении. Модуль вектора 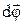равен углу поворота за интервал времени 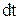. Линейное перемещение вектора 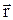за время dt

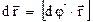(1.18)

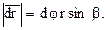
Вектор линейной скорости

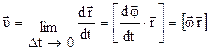, (1.19)

где 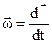– вектор угловой скорости.

Вектор угловой скорости 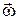совпадает с направлением вектора .

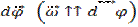Модуль вектора линейной скорости

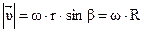(1.20)

Где 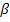- угол между векторам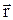и и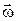

Вектор линейного ускорения

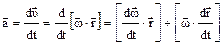
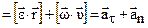, (1.21)

где 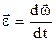– вектор углового ускорения,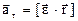– вектор касательного ускорения, 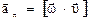– вектор нормального ускорения.

Направление вектора углового ускорения 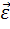совпадает с направлением вектора 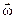(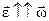),, если угловая скорость возрастает, и противоположно (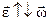), если она уменьшается.

Модули векторов ,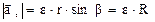

.

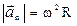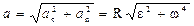. (1.22)

Угловой путь м.т., движущейся по окружности за время dt

.

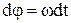Угловой путь 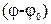точки за интервал времени 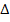t при начальном угле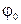

.

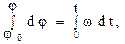
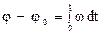При постоянной угловой скорости 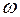, угловой путь и угол поворота определяется из равенств:

,

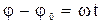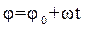(1.23)

При равноускоренном вращении точки для t=0, 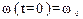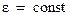, угловая скорость определяется из соотношения

,

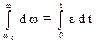
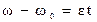
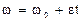Для равноускоренного вращения за время t угловой путь и угол поворота определяются из соотношений

,

,

,

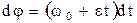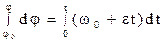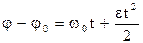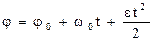. (1.24)

Для равнозамедленного вращения

,

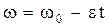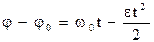, (1.25)

.

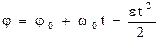Согласно определению угловая скорость измеряется в рад/с, угловое ускорение – рад/с².