2014-02-13
493
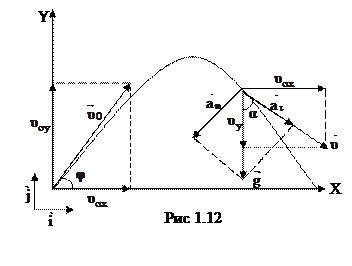
Частным случаем ускоренного движения является движение тела брошенного со скоростью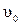 
под углом 
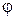к горизонту и падающего с постоянным ускорением свободного падения 
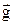(рис 1.12). Положение тела в пространстве определяется путем разложения его движения на равномерное прямолинейное по оси OX со скоростью 
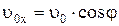и равнопеременное по оси OY с ускорением свободного падения g и начальной скоростью 
.
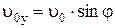В момент времени t координаты тела
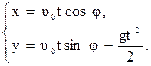(1.42)
вектор скорости
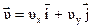. (1.43)
Модуль вектора скорости
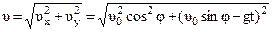(1.44)
где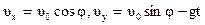 
.
Уравнение траектории найдём путем исключения параметра t из равенств (1.44)
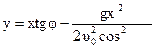. (1.45)
Ускорение свободного падения в любой точке траектории можно разложить на его касательную и нормальную составляющие, где модуль касательного ускорения
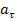
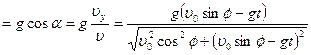, (1.46)
где α-угол между векторами скорости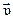 
и ускорения g в заданной точке траектории
Модуль нормального ускорения
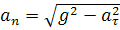. (1.47)
Из сравнения уравнения параболы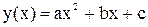 
и равенства (1.22) следует, что тело, брошенное под углом к горизонту, движется по параболе.
