2014-02-13
1141
Для самостоятельного изучения
Модули касательного и нормального ускорения находятся из соотношения
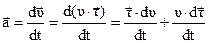, (1.38)
где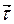 
единичный вектор, направленный по касательной к точке траектории в сторону движения м.т. (рис 1.11), а 
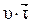- вектор мгновенной скорости 
.
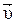Первое слагаемое в (1.11) равно касательному ускорению,
, 
,
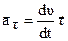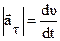
второе - нормальному
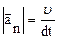(1.39)
Вектор касательного ускорения может совпадать с вектором мгновенной скорости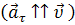 
и может быть ему антипараллелен 
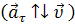. В первом случае движение будет ускоренным, а во втором – замедленным.
Рассмотрим перемещение материальной точки по траектории из точки 
в точку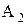
. (рис 1.7) За малый интервал времени 
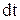единичный вектор в точке А2 равен сумме
,
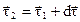где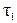 
– единичный вектор, определяющий направление движения в точке А1, 
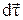– вектор изменения направления движения. Треугольник 
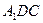, образованный векторам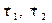и 
и 
, равнобедренный, т.к.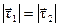 
=1. При 
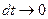, угол 
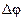между векторам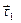и 
и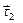 
уменьшается и стремится к нулю, а угол 
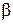между векторам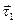и 
и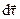 
увеличится до 
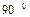. Следовательно, вектора и 
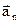направлены к центру кривизны траектории и совпадает с вектором нормали к скорости 
(
).
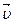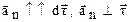Модуль вектора нормального ускорения определяется из треугольников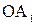 
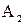и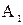 
DC. Эти треугольники равнобедренные и подобные, т.к. при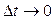 
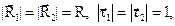где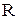 
– радиус кривизны траектории. Из соотношения сторон треугольников
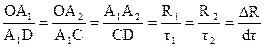. (1.40)
Для бесконечного малого интервала времени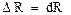
, 
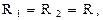
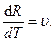
Вектор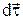 
можно представить в виде 
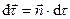. Тогда вектор нормального ускорения
, 
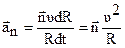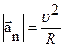(1.41)
