Материальная точка может участвовать одновременно в нескольких колебательных движениях. Сложить два или несколько колебаний – значит найти закон, которому подчиняется результирующее движение, найти траекторию этого движения материальной точки.
Сложение колебаний м.т. проводится геометрически, введением понятия амплитуды.
Вектор амплитуды 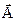 - это вектор, модуль которого равен амплитуде рассматриваемого колебания.
- это вектор, модуль которого равен амплитуде рассматриваемого колебания.
Если вектор амплитуды привести во вращение вокруг точки О, с угловой скоростью 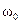 , то проекция конца этого вектора на ось х будет совершать гармонические колебания с циклической частотой
, то проекция конца этого вектора на ось х будет совершать гармонические колебания с циклической частотой 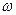 :
:
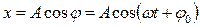 ,
,
где 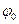 – угол, образованный вектором амплитуды и осью х в начальный момент времени. Сложим два гармонических колебания вдоль оси X (рис 1.13.
– угол, образованный вектором амплитуды и осью х в начальный момент времени. Сложим два гармонических колебания вдоль оси X (рис 1.13.
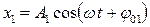 ;
;

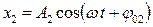 ;
;
где 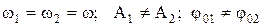
Так как колебания происходят вдоль одной прямой, то результирующая координата:
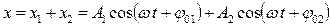 .
.
Вектор результирующей амплитуды 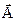 равен геометрической сумме векторов
равен геометрической сумме векторов 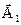 и
и 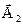 . Проекция конца вектора
. Проекция конца вектора 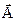 определяет результирующая координате x. Так как оба вектора,
определяет результирующая координате x. Так как оба вектора, 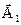 и
и 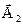 , вращаются в процессе колебаний с угловой скоростью
, вращаются в процессе колебаний с угловой скоростью 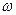 , с такой же скоростью будет вращаться и вектор результирующей амплитуды
, с такой же скоростью будет вращаться и вектор результирующей амплитуды 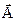 .
.
Для времени t=0
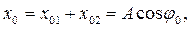
для произвольного момента времени t
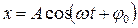 ,
,
где 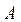 и
и 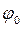 - амплитуда и начальная фаза результирующего колебания.
- амплитуда и начальная фаза результирующего колебания.
Из 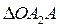 по теореме косинусов находим амплитуду и начальную базу колебания:
по теореме косинусов находим амплитуду и начальную базу колебания:
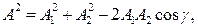
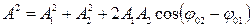 ,
,
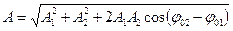 ,
,
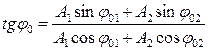 , (1.48)
, (1.48)
где 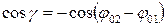 .
.
Амплитуда результирующего колебания зависит от разности фаз 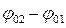 слагаемых колебаний. Если
слагаемых колебаний. Если 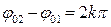 , где
, где 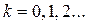 , то
, то 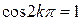 и
и 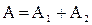 . Колебания усиливают друг друга.
. Колебания усиливают друг друга.
Если 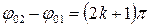 , то
, то 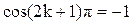 и
и 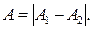 Если разность фаз равна нечётному числу
Если разность фаз равна нечётному числу 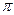 , колебания гасят друг друга. В зависимости от разности фаз амплитуда колебаний может принимать любые значения, лежащие в интервале
, колебания гасят друг друга. В зависимости от разности фаз амплитуда колебаний может принимать любые значения, лежащие в интервале
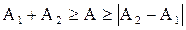 .
.
Рассмотрим сложение двух гармонических колебаний слегка отличающимися частотами, происходящих вдоль одной прямой для нескольких условий:
1. Пусть 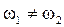 , причём
, причём 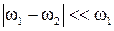 (или
(или 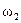 ),
), 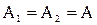 и
и 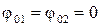
Уравнение колебаний:
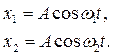
Координата результирующего колебания
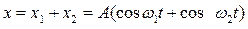 (1.49)
(1.49)
Так как 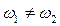 , то векторы амплитуды вращаются с разными угловыми скоростями.
, то векторы амплитуды вращаются с разными угловыми скоростями.
Сумма косинусов и координата определяются из соотношений:
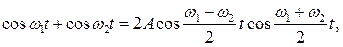
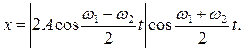
Выделенный множитель изменяется с течением времени гораздо медленнее, чем второй множитель. За время, в течение которого второй множитель совершает полное колебание, первый почти не изменяется (так как по условию 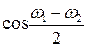 <<
<<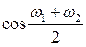 ). Это позволяет рассматривать колебание как гармоническое с частотой
). Это позволяет рассматривать колебание как гармоническое с частотой 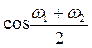 , у которого амплитуда
, у которого амплитуда 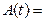
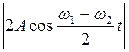 .
.
|
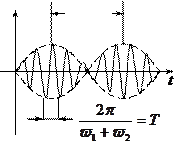
Гармонические колебания с периодически изменяющейся амплитудой называются биениями.
Частота и период биений
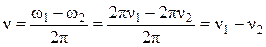 ,
, 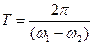
где 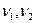 - частоты слагаемых колебаний. Следовательно, чем меньше отличаются частоты, тем меньше частота биений.
- частоты слагаемых колебаний. Следовательно, чем меньше отличаются частоты, тем меньше частота биений.

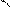 Точка одновременно участвует в двух колебаниях, происходящих вдоль координатных осей x и y, причём
Точка одновременно участвует в двух колебаниях, происходящих вдоль координатных осей x и y, причём
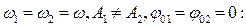
Уравнения для координат точки.
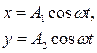
Разделив второе уравнение на первое, получим
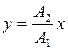
 Полученное соотношение представляет прямую, проходящую
Полученное соотношение представляет прямую, проходящую
через начало координат и наклонённую к оси х под углом
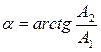 .
.
Точка будет совершать гармоническое колебание вдоль этой прямой:
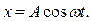
где 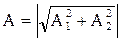 - амплитуда колебания.
- амплитуда колебания.
- При сложении колебаний, когда
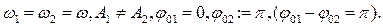
Уравнение для координат точки.
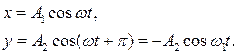
Разделив одно уравнение на другое, получим уравнение прямой с отрицательным тангенсом угла наклона.
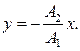
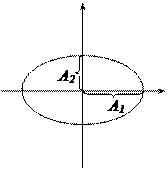 Для
Для 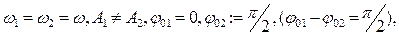
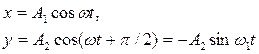
Перепишем эти уравнения в виде
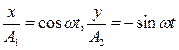
Возведём в квадрат и почленно сложим:
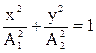
Полученное уравнение есть уравнение эллипса. Полуоси этого эллипса равны соответствующим амплитудам колебаний 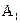 и
и 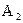 . При
. При 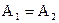 эллипс превращается в окружность.
эллипс превращается в окружность.
Если равность фаз слагаемых колебаний равна 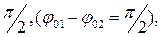 то движение по эллипсу (или по окружности) будет происходить по часовой стрелке.
то движение по эллипсу (или по окружности) будет происходить по часовой стрелке.
Если 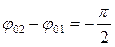 , движение происходит против часовой стрелки.
, движение происходит против часовой стрелки.
При сложении взаимно перпендикулярных гармонических колебаний с неодинаковыми циклическими частотами результирующее движение будет происходить по сложным траекториям, называемым фигурами Лиссажу. Форма фигур Лиссажу зависит от соотношения частот складываемых колебаний и разности их начальных фаз.
 2014-02-13
2014-02-13 4502
4502
