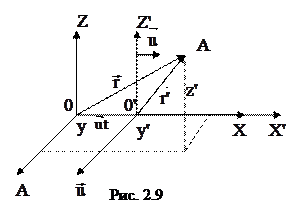Принцип относительности Галилея. Неинерциальные системы отсчета

Механическое движение в инерциальных системах отсчета одинаково и никаким опытом невозможно установить, покоится данная система отсчета или движется прямолинейно и равномерно.

Рассмотрим систему отсчета 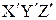, движущуюся относительно инерциальной системы X,Y,Z с постоянной скоростью 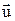(рис. 2.9). Пусть в начальный момент времени t = 0 системы отсчета совпадают. При движении системы отсчета Х`Y`Z`, радиус-вектор материальной точки в момент времени t в системе X,Y,Z равен

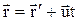, (2.5)

где 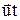– вектор перемещения системы по оси OX.

Продифференцируем полученное соотношение и запишем соотношение для скорости м.т. в системе X,Y,Z

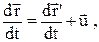
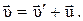(2.40)

Равенство (2.41) называется правилом сложения скоростей. Ускорения материальной точки в системах отсчета, движущихся относительно друг друга прямолинейно с постоянной скоростью будут равны:

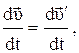(2.41)

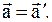
На м.т. в системе X,Y,Z действует сила 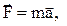а в системе Х`Y`Z` 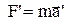. Из-за равенства ускорений следует, что эти силы равны. Следовательно, законы динамики не изменяются при переходе от одной системы к другой, а система отсчета, находящаяся в покое или движущаяся равномерно и прямолинейно относительно инерциальной системы, сама является инерциальной. Рассмотрим другой случай, когда система 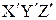движется относительно системы X,Y,Z со скоростью изменяющейся со временем u(t). В соответствии с правилом сложения скоростей

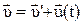. (2.42)

Продифференцируем последнее равенство по времени

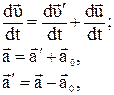(2.43)

где а₀ – ускорение движущейся системы отсчета, Х`Y`Z`,

а' – ускорение материальной точки в ней.

Ускорение материальной точки в системах отсчета, движущихся относительно друг друга с изменяющейся скоростью неодинаково, и, следовательно, неодинаковы и силы 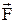,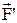действующие на нее.

Если обозначить силу, действующую на материальную точку массой m через 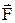, то в системе 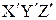ее ускорение

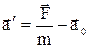. (2.44)

При умножении левой и правой части последнего равенства на m получим

,

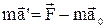где при ,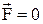

.

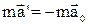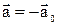Из последних соотношений следует, что при отсутствии силы 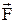, материальная точка в движущейся системе все равно будет двигаться с ускорением 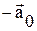, то есть так, как если бы на нее действовала сила. Эта сила называется силой инерции, обозначается .

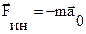Систему отсчета, движущуюся с ускорением относительно инерциальной системы, называют неинерциальной.

Для неинерциальных систем отсчета справедливо соотношение

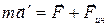. (2.45)