Кольцо
Числовые кольца и поля
Тема 1 Математические структуры
Опорный конспект лекций
дисциплины
«Алгебра и геометрия»
для студентов 1-го курса дневной
и 2-го курса заочной
форм обучения
специальностей «информатика»,
«прикладная математика»
Составитель: кандидат физ.-мат. наук, доцент Кудряшов Ю. Л.
Симферополь 2010
Определение 1.1: Непустое множество чисел называется кольцом, если это множество содержит произведение, сумму и разность любых двух чисел из этого множества.
Определение 1.2: Числовым полем называется числовое кольцо, которое содержит частное любых двух чисел из этого множества, (кроме деления на 0).
Теорема 1.1: Поле рациональных чисел содержится во всяком числовом поле, (то есть поле рациональных чисел – это минимальное числовое поле).
Пусть 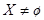 – множество элементов произвольной природы. Обозначим
– множество элементов произвольной природы. Обозначим 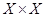 – декартово произведение, то есть множество упорядоченных пар
– декартово произведение, то есть множество упорядоченных пар 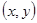 ,
, 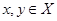 .
.
Определение 1.3: Пусть каждой паре 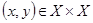 поставлен в соответствие один, вполне определенный, элемент из
поставлен в соответствие один, вполне определенный, элемент из 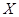 (то есть задано отображение:
(то есть задано отображение: 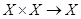 ). Тогда говорят, что на множестве
). Тогда говорят, что на множестве 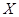 задана бинарная алгебраическая операция.
задана бинарная алгебраическая операция.
Будем операцию обозначать значком 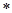 , где
, где 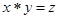 , то есть
, то есть 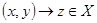 .
.
Определение 1.4: Множество 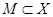 называется замкнутым относительно операции
называется замкнутым относительно операции 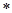 , если
, если 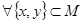 выполняется:
выполняется: 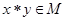 и
и 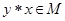 .
.
Определение 1.5: Множество 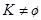 называется кольцом, если в нем определены две бинарные алгебраические операции
называется кольцом, если в нем определены две бинарные алгебраические операции 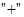 и
и 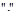 , удовлетворяющие следующим условиям:
, удовлетворяющие следующим условиям:
1. Операции 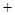 и
и  коммутативны, то есть
коммутативны, то есть 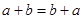 ,
, 
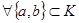 .
.
2. Операции 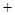 и
и 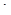 ассоциативны, то есть
ассоциативны, то есть 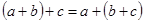 ,
, 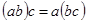 ,
, 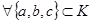 .
.
3. Операции 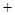 и
и 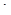 связаны законом дистрибутивности:
связаны законом дистрибутивности: 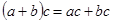 .
.
4. Операция 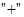 имеет обратную операцию, (которую мы обозначим
имеет обратную операцию, (которую мы обозначим 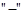 ). Это означает следующее:
). Это означает следующее: 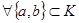
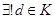 такой, что
такой, что 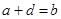 , (
, (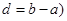 .
.
Все числовые кольца являются кольцами. Операции 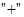 ,
, 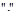 и
и 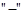 будем в дальнейшем называть соответственно сложением, умножением и вычитанием.
будем в дальнейшем называть соответственно сложением, умножением и вычитанием.
1. В кольце определено сложение и умножение любого конечного числа элементов кольца.
2. 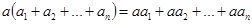 .
.
3. Закон дистрибутивности для разности, то есть 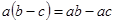 .
.
4. В каждом кольце существует единственный нулевой элемент, который обозначим 0 такой, что 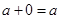 ,
, 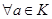 .
.
5. 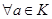 существует единственный противоположный элемент
существует единственный противоположный элемент 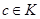 такой, что
такой, что  . Обозначается
. Обозначается 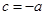 .
.
6. 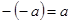 .
.
7. 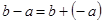 .
.
8. 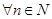 ,
, 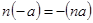 .
.
9. 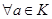 ,
, 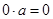 .
.
10. Правила знаков: 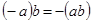 и
и 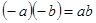 .
.
Определение 1.6: Элементы  ,
, 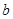 из кольца
из кольца 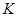 называются делителями нуля, если
называются делителями нуля, если 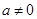 ,
, 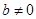 , но
, но 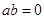 .
.
 2014-02-13
2014-02-13 1272
1272