Поле
Определение 1.7: Кольцо 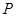 называется полем, если
называется полем, если 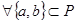 ,
, 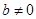 ,
, 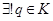 такой, что
такой, что 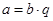 ,
, 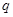 называется частным элементов
называется частным элементов  ,
, 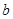 и обозначается
и обозначается  .
.
Для поля выполнены все свойства кольца.
1. 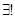 единичный элемент, который обозначим
единичный элемент, который обозначим 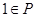 такой, что
такой, что 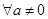 ,
, 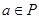 ,
, 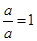 .
.
2. 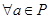 ,
, 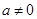 существует обратный элемент, который обозначим
существует обратный элемент, который обозначим 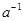 такой, что
такой, что 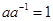 .
.
3. 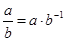 .
.
4. 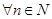 ,
, 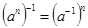 ,
, 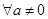 . Положим
. Положим 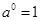 .
.
5. 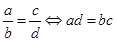 .
.
6. 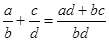 ,
, 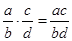 .
.
Определение 1.8: Пусть 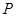 – поле, множество
– поле, множество 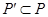 называется подполем поля
называется подполем поля 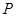 , а
, а 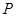 называется расширением поля
называется расширением поля 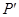 , если
, если 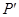 является полем относительно тех же операций
является полем относительно тех же операций 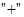 и
и 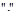 , относительно которых
, относительно которых 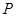 является полем.
является полем.
Возьмем 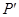 – подполе поля
– подполе поля 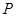 , рассмотрим элемент
, рассмотрим элемент 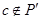 и
и 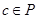 .
.
Множество 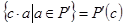 – является подполем и называется полем, полученным из поля
– является подполем и называется полем, полученным из поля 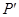 присоединением к нему элемента
присоединением к нему элемента 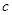 .
.
Определение 1.9: Кольца 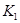 и
и  называются изоморфными (
называются изоморфными (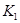 ~
~ ), если существует взаимно-однозначное отображение
), если существует взаимно-однозначное отображение 
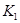 на
на  такое, что
такое, что 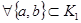 ,
, 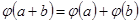
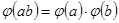
 2014-02-13
2014-02-13 478
478








