Схема решения системы линейных уравнений
1. Вычисляем 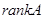 и
и 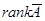 , если
, если 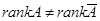 , то система несовместна.
, то система несовместна.
Если 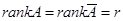 , то:
, то:
2. Выбираем минор порядка 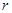 в матрице
в матрице  , который отличен от нуля.
, который отличен от нуля.
3. Рассматриваем систему из уравнений, коэффициенты которых входят в выбранный минор. Неизвестные, которые не входят в выбранный минор переносим в правые части уравнений и считаем эти неизвестные свободными.
4. Решаем систему из 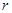 уравнений с
уравнений с 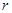 неизвестными по правилу Крамера.
неизвестными по правилу Крамера.
Определение 6.3: Система (1) называется системой линейных однородных уравнений, если 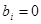 ,
, 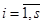 . (С.Л.О.У.)
. (С.Л.О.У.)
Теорема 6.2: Множество решений С.Л.О.У. образует в 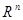 подпространство.
подпространство.
Определение 6.4: Максимальная линейно независимая система решений С.Л.О.У. называется фундаментальной системой решений, (то есть базис подпространства решений).
Теорема 6.3: Если 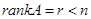 , (где
, (где  – матрица С.Л.О.У.), то фундаментальная система решений состоит из
– матрица С.Л.О.У.), то фундаментальная система решений состоит из 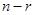 векторов пространства
векторов пространства 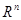 .
.
 2014-02-13
2014-02-13 581
581








