Определение 5.8: Пусть 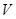 – подпространство в
– подпространство в 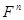 . Система векторов
. Система векторов 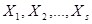 из
из 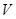 называется базисом подпространства
называется базисом подпространства 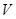 , если она удовлетворяет двум условиям:
, если она удовлетворяет двум условиям:
1. Система линейно независима.
2.  .
.
Из определения 5.8 следует, что 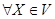 ,
, 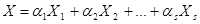 .
.
Определение 5.9: Система чисел 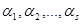 называется координатами вектора
называется координатами вектора 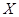 в базисе
в базисе 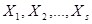 .
.
Теорема 5.2: Система векторов 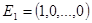 ,
, 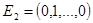 ,…,
,…, 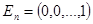 образует базис пространства
образует базис пространства 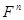 .
.
Лемма: Пусть 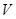 – подпространство в
– подпространство в 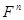 ,
,  – базис в
– базис в 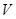 ,
, 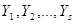 – линейно независимая система векторов из
– линейно независимая система векторов из 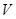 , тогда
, тогда 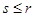 .
.
Теорема 5.3: Всякое подпространство 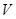 из
из 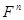 обладает базисом, при этом все базисы подпространства
обладает базисом, при этом все базисы подпространства 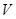 состоят из одинакового количества векторов.
состоят из одинакового количества векторов.
Определение 5.10: Количество векторов в базисе подпространства 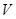 называется размерностью подпространства и обозначается
называется размерностью подпространства и обозначается 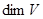 .
.
Определение 5.11: Ранг системы векторов 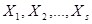 – это максимальное число линейно независимых векторов в этой системе. Обозначается:
– это максимальное число линейно независимых векторов в этой системе. Обозначается: 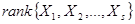 . Очевидно, что
. Очевидно, что 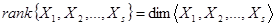 .
.
 2014-02-13
2014-02-13 4320
4320
