Тема 7 Алгебра матриц
Рассмотрим множество матриц порядка 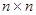 с элементами из
с элементами из  , которое обозначим
, которое обозначим 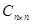 .
.
Пусть 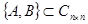 и
и 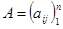 ,
, 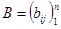 .
.
Определение 7.1: 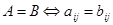 ,
, 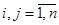 .
.
Введем во множестве 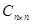 следующие операции:
следующие операции:
1. 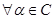 ,
, 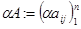 .
.
2. 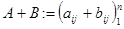 .
.
3. 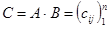 , где
, где 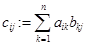 ,
, 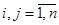 .
.
Теорема 7.1: Умножение матриц некоммутативно и ассоциативно.
Теорема об умножении определителей: 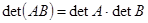 .
.
Определение 7.2: Матрица  называется невырожденной, если
называется невырожденной, если 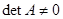 .
.
Определение 7.3: Матрица 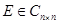 называется единичной, если
называется единичной, если 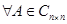 выполняется:
выполняется: 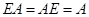 .
.
Теорема 7.2: Во множестве 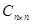 существует единственная единичная матрица и
существует единственная единичная матрица и 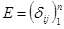 , где
, где 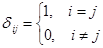 .
.
Определение 7.4: Матрица 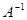 называется обратной для матрицы
называется обратной для матрицы  , если
, если 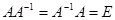 .
.
Определение 7.5: Матрица 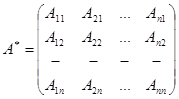 , где
, где 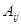 – алгебраическое дополнение к элементам
– алгебраическое дополнение к элементам 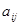 матрицы
матрицы  .
.
Определение 7.6: Матрица 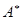 называется присоединенной матрицей.
называется присоединенной матрицей.
Теорема 7.3: 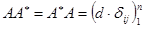 , где
, где 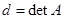 .
.
Следствие: Если 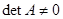 , то
, то 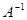 существует и
существует и 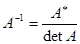 .
.
Тема 8 Полиномы (многочлены)
Определение 8.1: Полиномом называется выражение вида 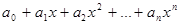 , где
, где 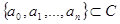 – коэффициенты. Если
– коэффициенты. Если 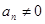 , то это полином
, то это полином  -ой степени.
-ой степени.
Таким образом, все числа, кроме 0, являются полиномами 0-ой степени, а само число 0 – это полином, степень которого не определена.
Определение 8.2: Два полинома называются равными, если равны их коэффициенты при одинаковых степенях 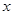 .
.
 2014-02-13
2014-02-13 603
603








