Рассмотрим матрицу  размерности
размерности 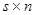 :
:
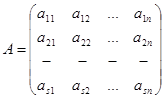 .
.
Определение 6.1: Рангом матрицы  по столбцам (
по столбцам (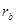 ) называется ранг ее системы столбцов как векторов пространства
) называется ранг ее системы столбцов как векторов пространства 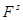 . Рангом матрицы
. Рангом матрицы  по строкам (
по строкам (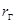 ) называется ранг ее системы строк как векторов пространства
) называется ранг ее системы строк как векторов пространства 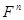 .
.
Определение 6.2: Выберем в матрице  произвольные
произвольные 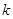 строк и
строк и 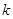 столбцов,
столбцов, 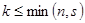 . Элементы, стоящие на пересечении этих строк и столбцов, образуют квадратную матрицу
. Элементы, стоящие на пересечении этих строк и столбцов, образуют квадратную матрицу 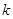 -го порядка, определитель которой называется минором
-го порядка, определитель которой называется минором 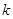 -го порядка матрицы
-го порядка матрицы  .
.
Лемма: Если все миноры 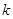 -го порядка матрицы
-го порядка матрицы  равны нулю, то равны нулю все миноры более высоких порядков.
равны нулю, то равны нулю все миноры более высоких порядков.
Теорема 6.1: Наивысший порядок отличных от нуля миноров матрицы  равен ее рангу по столбцам.
равен ее рангу по столбцам.
Следствие 1: 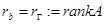 – ранг матрицы.
– ранг матрицы.
Следствие 2: Определитель равен нулю тогда и только тогда, когда его строки (столбцы) линейно зависимы.
Пусть дана система 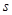 линейных уравнений с
линейных уравнений с  неизвестными:
неизвестными:
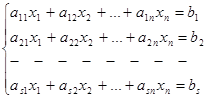 (1)
(1)
Составим матрицу системы: 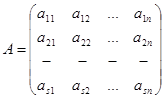 и расширенную матрицу системы:
и расширенную матрицу системы: 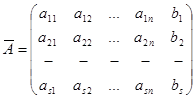
Теорема Кронекера-Капелли: Система (1) совместна тогда и только тогда, когда 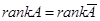 .
.
 2014-02-13
2014-02-13 1038
1038
