2014-02-09
1007
Методы определения свойств объекта
1. Аналитические методы – методы на основе математического описания объекта.
Достоинства:
Ø Математическое описание составляется на основе теоретического анализа химических и физических процессов, протекающих в объекте.
Ø Можно прогнозировать работу объекта в статических и динамических режимах.
Недостатки:
Ø Трудоемкость решения уравнений математического описания сложных объектов.
Ø Точность математического описания зависит от степени изученности объекта и от уровня управляющих воздействий.
На инженерном уровне можно ориентировочно оценить параметры объекта ни основе уравнений динамики и статики материальных и тепловых потоков.
2. Экспериментальные методы – состоят в определении характеристик объекта путем постановки на нем специального эксперимента.
Достоинства:
Ø Простота.
Ø Возможность определения свойств конкретного объекта.
Недостатки:
Ø Невозможно выявить функциональные связи между входными и выходными переменными в широком диапазоне.
При проведении эксперимента на объект наводят типовые возмущения:
Ø Ступенчатое,
Ø Импульсное,
Ø Синусоидальное.
Обработка эксперимента называется идентификацией, которая подразделяется на:
1. Структурную – определение структуры и параметров модели объекта на основе экспериментальных данных;
2. Параметрическую – определение параметров модели объекта на основе экспериментальных данных.
(при ступенчатом входном воздействии).
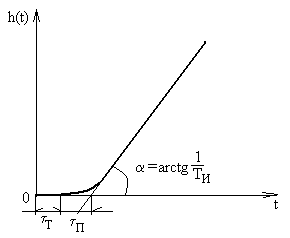Структурная идентификация:
Объект аппроксимируется моделью, состоящей из звена чистого запаздывания и идеального интегрирующего звена.
Передаточная функция модели объекта:
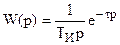
Параметрическая идентификаци я включает следующие этапы графической идентификации:
1. выделение чистого запаздывания tТ;
2. построение линии вдоль участка характеристики, изменяющего с постоянной скоростью до пересечения с осью времени;
3. выделение переходного запаздывания tП;
4. определение общего запаздывания: t= tТ + tП;
5. определение постоянной времени интегрирования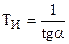 
.
Методы идентификации экспериментальных данных состоят не только из графических интерпретаций. Объект может аппроксимироваться звеном произвольного порядка, а сам метод сводится к оценки коэффициентов дифференциального уравнения путем многократного интегрирования экспериментальных данных.
Используются также интерполяционные методы.
Эти методы реализуются по нормализованным экспериментальным характеристикам, полученным на основе исходной кривой разгона.
