Поскольку энергетический спектр электронов носит зонный характер, определим зависимость энергии электронов Е от импульса р внутри каждой зоны. Зависимость Е(р) называют дисперсионным соотношением.
Движение совершенно свободного электрона вдоль оси X описывается уравнением Шредингера
¶2Y/¶x2 +(2m/ħ2 )EY=0 (4.1)
где E=P2/2m (т.к. он обладает только кин. энергией) (4.2)
Формула (4.2) представляет собой дисперсионное соотношение для свободных электронов Е(р). Преобразуем его по формуле де Бройля:
P = h/l= ħ / (l/2p) = ħk, (4.3)
где l- длинна волны,
k=2 p/l - значение волнового вектора электрона. (4.4)
Волновой вектор k по направлению совпадает с направлением распространения электронной волны.
Подставим Р из (4.3) в (4.2):
E = ħ2k2/2m (4.5)
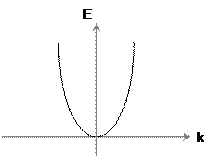
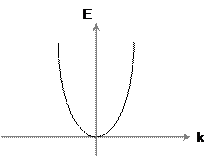 Из формул (4.5) и (4.2) видно, что для свободных электронов закон дисперсии имеет квадратичный характер и для одномерного движения выражается параболой (рис 4.4).
Из формул (4.5) и (4.2) видно, что для свободных электронов закон дисперсии имеет квадратичный характер и для одномерного движения выражается параболой (рис 4.4).
Рисунок 4.4
Решением уравнения Шредингера (4.1) является плоская бегущая волна
Y=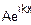 (4.6)
(4.6)
Квадрат модуля волновой функции пропорционален вероятности обнаружения электрона в той или иной области пространства. Как видно из (4.6)
для свободного электрона эта вероятность не зависит от координат электрона, т.к. ½Y½2=Y×Y* = A2 (4.7)
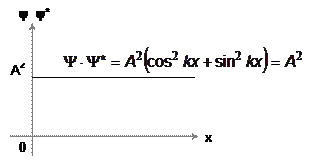 Это означает, что для свободного электрона все точки пространства эквивалентны и вероятность нахождения его в любой из них одинакова (рис.4.5).
Это означает, что для свободного электрона все точки пространства эквивалентны и вероятность нахождения его в любой из них одинакова (рис.4.5).
Рисунок 4.5
Однако для электрона, движущегося в периодическом поле кристалла, вероятность обнаружения его в данном месте кристалла должна быть периодической функцией, зависящей от координаты x. Периодичность функции кратна постоянной решетки а. Различными вероятностями будут обладать только положения электрона в пределах одного периода, т.е. амплитуда волновой функции электрона, движущегося в периодичном поле, не остается постоянной, а периодически меняется с периодом, равным периоду решетки а. Обозначим эту амплитуду U(x). Тогда волновая функция электрона, движущегося в периодическом поле кристалла в направлении x, будет:
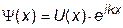 (4.8)
(4.8)
где U(x+na)=U(x), n - любое целое число.
|
|
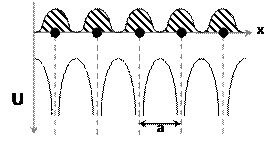 .
. Рисунок 4.6
Соответственно должно изменяться и дисперсионное соотношение для электронов движущихся в периодическом поле кристалла. Во-первых, энергетический спектр таких электронов приобретает зонный характер, во – вторых, внутри каждой зоны энергия электрона оказывается периодической функцией волнового вектора k. Для одномерного кристалла с параметром а энергия может быть выражена следующим соотношением:
E(k)=Ea+C+2Acos(ka) (4.9)
Ea – энергия атомного уровня, из которого образовалась зона;
С – сдвиг уровня под действием поля соседних атомов;
А – так называемый обменный интеграл, учитывающий появившуюся у электронов кристалла возможность перехода от атома к атому, вследствие перекрытия их волновых функций. Он тем больше, чем сильнее перекрываются волновые функции, т.е. с чем большей частотой могут обмениваться соседние атомы своими электронами.
Для s состояний As<0; для p состояний Ap>0.
Поэтому уравнение (4.9):
- для s зон Es(k)=E`s – 2Ascos(ka) (4.10)
- для p зон Ep(k)=E`p – 2Apcos(ka) (4.11)
где E`s=Eas+Cs; E`p=Eap+Cp;
As и Ap – абсолютные значения обменных интегралов для этих состояний.
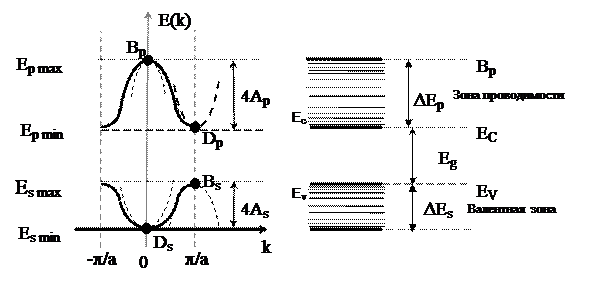 На рис.4.7 изображены дисперсные кривые E(k) для s и p зон, построенные по уравнениям (4.10) и (4.11).
На рис.4.7 изображены дисперсные кривые E(k) для s и p зон, построенные по уравнениям (4.10) и (4.11).
Рисунок 4.7
Области значений волнового вектора k, в пределах которых энергия Е(k) электрона, как периодическая функция, проходит полный цикл изменения, называют зонами Бриллюэна.
Для одномерного кристалла первая зона Бриллюэна располагается от k= +p/a до k= -p/a и имеет протяженность 2p/a. Вблизи экстремума дисперсионную кривой (при k=0, k= ±p/a) cos(ka) можно разложить в ряд по ka и ограничиться первыми двумя членами разложения. Подставляя это в уравнение (4.10) и (4.11) получим:
Es(k)= Es min +As(ka)2 (4.12)
Ep(k)= Ep max +Ap(ka)2 (4.13)
Минимум дисперсной кривой Е(k) называют дном энергетической зоны, а максимум - вершиной. Поэтому полученные соотношения можно переписать следующим образом:
Eдно(k)= Emin + Aд(ka)2 (4.14)
Eверх(k)= Emax - Aв(ka)2 (4.15)
Таким образом, у дна и вершины энергетической зоны энергия электрона пропорциональна квадрату волнового вектора и обменному интегралу, определяющему ширину зоны. На рисунке 4.7 параболы, соответствующие уравнениям (4.14) и (4.15), показаны пунктирными линиями. Для реальных кристаллов зависимость Е(k) является более сложной.
 2014-02-09
2014-02-09 6240
6240

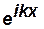 и удовлетворяет условию периодичности, называется функцией Блоха.
и удовлетворяет условию периодичности, называется функцией Блоха.