Энергетические зоны кристалла

Взаимодействие каждого электрона с остальными рассматривается как взаимодействие его с усредненным пространственным распределением заряда электронов. Это поле создается усредненным в пространстве зарядом всех других электронов и всех ядер.

Медленное движение ядер рассматривается в поле среднего пространственного распределения заряда электронов (т.е. без учета поля, создаваемого мгновенным расположением электронов).

При описании движения электрона ядра считаются неподвижными (из-за очень большой разницы в массах и скоростях движения).

Основные положения

Глава 4. Зонная теория твердых тел

Для определения свойств кристалла нужно знать характер взаимодействия всех составляющих его частиц (ядер, электронов). Точное их описание практически невозможно из-за большого количества (≈10²⁸ в 1м³) и непрерывного движения.

Для описания многих свойств необходимо знать только состояния всех валентных электронов (многоэлектронная задача), что упрощает изучение свойств кристалла. Ряд дополнительных упрощений сводит многоэлектронную задачу к одноэлектронной задаче движения одного электрона в электрическом поле кристалла, что позволяет решить для этого случая уравнение Шредингера. Упрощения заключаются в следующем:

Таким образом, в рамках зонной теории многоэлектронная задача сводится к задаче о движении одного электрона во внешнем периодическом поле - усредненном и согласованном поле всех ядер и электронов.

Состояние электрона в атоме определяется пятью основными квантовыми числами:

- главное квантовое число (n= 1; 2; 3…), определяющее энергию электрона в поле ядра (номер слоя);

- орбитальное квантовое число (l=0; 1; 2; 3…, соответственно s, p, d, f …), определяющее орбитальный момент количества движения электрона;

- магнитное квантовое число (m_l=0, ±1; ±2; ±3;…±l), определяющее ориентацию орбитального момента количества движения;

- спиновое квантовое число (s=1/2), определяющее собственный момент количества движения электрона;

- спиновое квантовое число (m_s=±1/2), определяющее ориентацию собственного момента количества движения электрона.

Изолированный атом является потенциальной ямой, в которой электрон может занимать одно из дискретных состояний (рис 4.1а). Если сблизить два атома на расстояние больше, чем 10^-9 м =10 Å (Ангстрем), то энергетические уровни электронов не изменятся (рис.4.1 б).

В твердом теле расстояния между атомами меньше 10^-9 м, поэтому каждый из них оказывается в достаточно сильном поле соседних атомов. Сближение атомов снижает высоту и уменьшает толщину потенциального барьера, отделяющего изолированные атомы друг от друга. Поэтому валентные электроны получают возможность практически беспрепятственно переходить от одного атома к другому. Скорость этого движения электронов ≈ 10⁵ м/с, поэтому валентный электрон находится в данном узле решетки в течение 10^-15 с. Это соответствует состоянию обобществления их в решетке (рис. 4.2).

Рисунок 4.2

Такие обобществленные электроны называются свободными. Вследствие резкого уменьшения толщины и высоты потенциального барьера свободу перемещения по кристаллу получают не только валентные электроны, но и электроны, расположенные на более низких уровнях. Это происходит путем туннельного перехода сквозь барьеры, отделяющие соседние атомы, хотя вероятность такого перехода существенно меньше.

Для изолированного атома данный энергетический уровень конкретного электрона является единственным. При сближении N таких же изолированных атомов и образовании решетки этот уровень повторяется N раз (N-кратное вырождение). Поскольку на каждый атом действует поле соседей, то происходит снятие вырождения путем расщепления этого уровня на N близко расположенных подуровней. Расстояние между ними мало (при числе атомов 10²⁸ и ширине зоны 1эВ расстояние между подуровнями ~10^-28 эВ). Они образуют энергетическую зону. Поскольку в каждом атоме кристалла несколько электронов, то в нем появляется система энергетических зон.

Ширина зоны зависит от природы атомов решетки и межатомных расстояний в ней. Несмотря на малое расстояние между подуровнями, число их конечно, что играет важную роль в распределении электронов по состояниям.

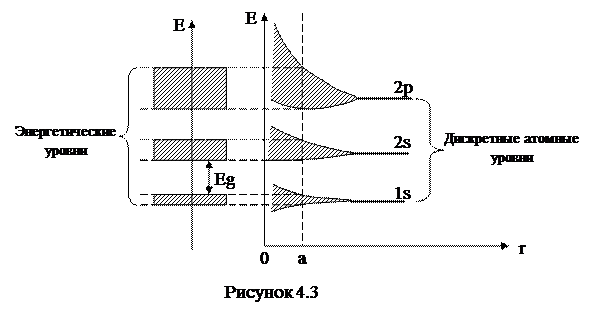Внутренние электроны, сильно связанные с ядром, испытывают незначительное возмущение от соседних атомов, поэтому их энергетические уровни остаются практически такими же узкими, как в изолированных атомах. На валентные электроны действует сильное поле решетки, поэтому их энергетические зоны оказываются наиболее широкими (рис.4.3).