Координатное описание треугольника

Задание графических элементов на плоскости

Параллельные плоскости - параллельными.

Плоскости после преобразования остаются плоскостями.

Отношения деления отрезков остаются неизменными.

Параллельные прямые - параллельными.

Прямые линии после преобразований остаются прямыми.

Эти операции называются аффинными преобразованиями. Различают двумерные и трехмерные аффинные преобразования.

Поворота изображения (употребляют также термины вращение, изменение ориентации).

Масштабирования (увеличения или уменьшения размеров) изображения;

Переноса (перемещения) изображения;

Создавать движущиеся изображения.

Уменьшать размер рисунка для внесения, например, поясняющих надписей или отображения на экране новых рисунков;

Увеличивать размер рисунка для улучшения его наглядности или отображения более мелких деталей;

Добавлять к существующему рисунку новые элементы;

Создавать рисунок из более мелких элементов (составных частей);

Перемещать рисунки из одного места экрана в другое;

Виды преобразований

Лекция 9 Геометрические преобразования графических элементов. Аффинные преобразования на плоскости

При построении изображений часто приходится иметь дело с ситуациями, когда общее изображение (рисунок) включает в себя целый ряд компонент (подрисунков), отличающихся друг от друга только местоположением, ориентацией, масштабом, т.е. отдельные подрисунки обладают значительным геометрическим сходством.

В этом случае целесообразно описать один подрисунок в качестве базового, а затем получать остальные требуемые подрисунки путем использования операций преобразования.

С помощью операций преобразования можно выполнять следующие действия:

Все изменения рисунков можно выполнить с помощью трех базовых операций:

Основные геометрические свойства двумерных аффинных преобразований:

Основные геометрические свойства трехмерных аффинных преобразований:

Возьмем на плоскости произвольную точку (обозна­чим ее через 0) и проведем через нее две взаимно пер­пендикулярные прямые.Выберем на каждой из этих прямых одно из возможных направлений и еди­ный масштабный отрезок. Назовем одну из оснащен­ных таким образом прямых осью абсцисс, или осью Ох, а другую - осью ординат, или осью Оу.

Предложенная конструкция позволяет поставить в соответствие каждой точке М рассматриваемой плоскости, упорядоченную пару чисел х и у - ее координат, являющихся проекциями этой точки на координатные оси Ох и Оу.

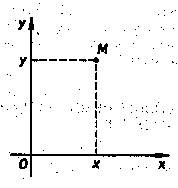
Тем самым на плоскости задана координатная система Оху, в ко­торой каждая точка М однозначно описывается своими координа­тами (х,у), что позволяет количественно описывать любые плоские геометрические фигуры.

Рассмотрим какую-нибудь простую геометрическую фигуру, ска­жем треугольник. Обозначим через М₁, Мг и Мз его вершины, а через х₁,у_1, х₂у₂, х₃у₃ - соответствующие координаты этих вершин.

Каждый треугольник однозначно определяется заданием своих вершин. Беря шестерку чисел х₁,у_1, х₂у₂, х₃у₃ и рассматривая их как соответствующие координаты точек, мы получаем три точки на плос­кости (рис. 1.1).

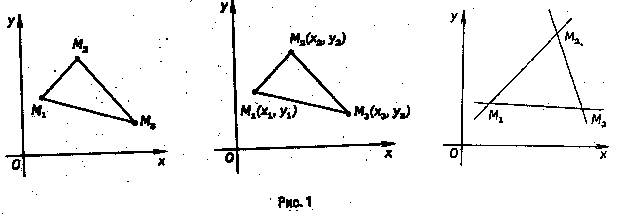
Конечно, эти точки определяют треугольник однозначно. Однако для того, чтобы описать все точки этого треугольника, необходимо построить еще его стороны, т.е. соединить точ­ки М1, М2 и Мз отрезками прямых (рис. 1.2).

Треугольник можно описать и другим способом, задавая его сторо­ны или, что то же самое, задавая пря­мые, на которых эти стороны лежат (рис. 1.3).