Инвертирующий усилитель. Теперь найдем выражение для коэффициента усиления инвертирующего усилителя

Теперь найдем выражение для коэффициента усиления инвертирующего усилителя. Как следует из самого названия, входной и выходной сигналы инвертирующего усилителя сдвину­ты по фазе на 180°. Здесь, как и в случае неинвертирующего усилителя, благодаря высокому коэффициенту усиления усилите­ля без обратной связи для изме­нения выходного напряжения уси­лителя во всем рабочем диапазо­не достаточно весьма малых зна­чений U _д. (Обычно U _{вых.макс} немного меньше напряжения питания.) Если на схему подать положительное U _вх, то U _д ста­нет положительным и выходной потенциал начнет снижаться (поскольку входное напряжение подано на инвертирующий вход усилителя). Выходное напряжение будет меняться в отрицательном направлении до тех пор, пока напряжение на инвер­тирующем входе (точка А на рис. 17) не станет почти нуле­вым: U _д = U _вых/ А ≈ 0. Таким образом, R ₁ и R _о.с действуют как делитель напряжения между U _вых и U _вх, и отношение U _вых/ U _вх равно таковому для R _о.с/ R ₁. Точку А часто называют потенциально заземленной, потому что ее потенциал почти ра­вен потенциалу земли, так как U _д, как правило, весьма мало.

Чтобы получить выражение для коэффициента усиления с обратной связью, еще раз напомним, что 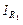=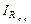, a R _вх усилителя велико. Поскольку 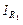= (U _вх – U _д)/ R ₁ и 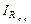= – (U _вх – U _д)/ R _о.с, можно написать, что (U _вх – U _д)/ R ₁ = – (U _вх – U _д)/ R _о.с. Знак минус перед правой частью этого равенства означает, что выход инвертирован. Полагая U _д = 0 (так как А →∞), получим U _вх / R ₁ = – U _вых/ R _о.с. Коэффициент усиления с обратной связью равен

K _о.с = U _вых/ U _вх = – R _о.с/ R ₁. (2)

Входное сопротивление схемы инвертирующего усилителя равно R ₁, в силу того что благодаря обратной связи в точке А на рис. 17 сохраняется приблизительно нулевой потенциал. Сопротивление R ₁ должно быть выбрано так, чтобы не нагру­жать источник напряжения U _вх, и, естественно, R _о.с должно быть достаточно большим, чтобы чрезмерное нагружать опе­рационный усилитель.