Усилитель с дифференциальным выходом (балансный)

Предположим сначала, что R ₁ = R ₂и R _о.с = R' _о.с и что на­пряжения на выводах инвертирующего и неинвертирующего входов усилителя на рис. 21 одинаковы и равны U _о.с. Послед­нее допущение является обоснованным, если, как и в случае усилителя с дифференциальным входом, предположить, что коэффициент усиления усилителя без обратной связи А весьма велик. Знак плюс около вывода вых.1 указывает, что U_A имеет полярность, противоположную U ₁,а знак минус около вывода вых.2 показывает, что полярность U_В противоположна поляр­ности U ₂.

Общее выходное напряжение является алгебраической суммой U_A и U_В. Заметим, что, если U ₁ = 0 и входом служит U ₂,то усилитель действует как инвертор с U_A = 0и U_В = - (R' _о.с/ R ₂) U ₂. Точно так же, если U ₂ =0, U_B = 0,a U_A = (R _о.с/ R ₁) U ₁,по существу получается тандем двух инверторов.

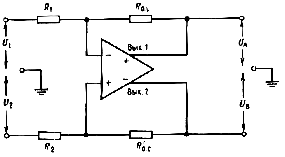
Рис.21. Усилитель с дифференциальным выходом

Выведем выражение для U _вых. Известно, что 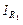= 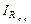и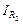 = 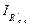;поэтому 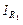= (U ₁ – U _о.с)/ R₁ = (U _о.с – U_А)/ R _о.с; 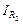= (U ₂ – U _о.с)/ R ₂ = (U _о.с – U_В)/ R' _о.с.

Вычитая первое уравнение из второго, получим с учетом равенства R ₁ = R ₂и R _о.с =R' _о.с

(U ₂ – U _о.с)/ R ₁ - (U ₁ – U _о.с)/ R ₁ = (U _о.с – U_В)/ R _о.с - (U_о.с – U_А)/ R _о.с;

(U ₂ – U ₁)/ R ₁ = (U_А – U_В)/ R _о.с.

Поскольку │ U_А – U_В │= U _вых,имеем

(U ₂ – U ₁)/ R ₁ = U _вых / R _о.с, U _вых = (R _о.с / R ₁)(U ₂ – U ₁). (4)