Системой счисления называется способ изображения чисел с помощью ограниченного набора символов, имеющих определенные количественные значения. Систему счисления образует совокупность правил и приемов представления чисел с помощью набора знаков (цифр).
Различают позиционные и непозиционные системы счисления. В позиционных системах каждая цифра числа имеет определенный вес, который зависит от позиции цифры в последовательности, изображающей число. Позиция цифры называется разрядом. В позиционной системе счисления любое число можно представить в виде:
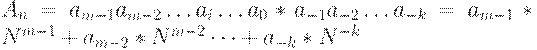
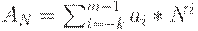 | (14.1) |
где 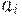 -
- 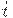 -я цифра числа;
-я цифра числа;
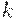 - количество цифр в дробной части числа;
- количество цифр в дробной части числа;
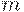 - количество цифр в целой части числа;
- количество цифр в целой части числа;
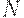 - основание системы счисления.
- основание системы счисления.
Основание системы счисления 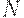 показывает, во сколько раз "вес"
показывает, во сколько раз "вес" 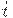 -го разряда больше (
-го разряда больше ( ) разряда. Целая часть числа отделяется от дробной части точкой (запятой).
) разряда. Целая часть числа отделяется от дробной части точкой (запятой).
Пример 14.1. 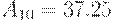 .
.
В соответствии с формулой (14.1) это число формируется из цифр с весами разрядов:
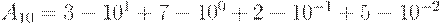
Теоретически наиболее экономичной системой счисления для представления значения числа цифрами является система с основанием 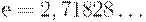 , находящимся между числами 2 и 3.
, находящимся между числами 2 и 3.
Во всех современных ЭВМ для представления числовой информации применяется двоичная система счисления. Это обусловлено:
- более простой реализацией алгоритмов выполнения арифметических и логических операций;
- более надежной физической реализацией основных функций, так как они имеют всего два состояния (0 и 1);
- экономичностью аппаратной реализации всех схем ЭВМ.
При  число различных цифр, используемых для записи чисел, ограничено множеством из двух цифр (нуль и единица). Кроме двоичной системы счисления, широкое распространение получили и производные системы:
число различных цифр, используемых для записи чисел, ограничено множеством из двух цифр (нуль и единица). Кроме двоичной системы счисления, широкое распространение получили и производные системы:
- двоичная -
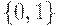 ;
; - десятичная, точнее двоично-десятичное представление десятичных чисел -
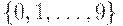 ;
; - шестнадцатеричная -
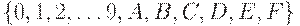 . Здесь шестнадцатеричная цифра
. Здесь шестнадцатеричная цифра 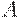 обозначает число 10,
обозначает число 10, 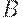 - число 11,...,
- число 11,..., 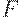 - число 15;
- число 15; - восьмеричная (от слова восьмерик) -
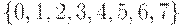 . Она широко используется во многих специализированных ЭВМ.
. Она широко используется во многих специализированных ЭВМ.
Восьмеричная и шестнадцатеричная системы счисления являются производными от двоичной, так как 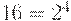 и
и 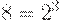 . Они применяются в основном для более компактного изображения двоичной информации, так как запись значения чисел производится существенно меньшим числом знаков
. Они применяются в основном для более компактного изображения двоичной информации, так как запись значения чисел производится существенно меньшим числом знаков
Пример 14.2. Число 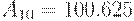 в двоичной, восьмеричной и шестнадцатеричной системах счисления имеют следующее представление:
в двоичной, восьмеричной и шестнадцатеричной системах счисления имеют следующее представление:
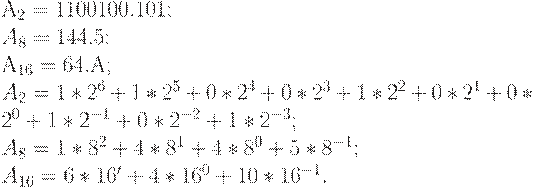
В табл. 14.1 приведено сравнительное представление чисел в различных системах счисления: десятичной (10 с/с), двоичной (2 с/с), восьмеричной (8 с/с) и шестнадцатеричной (16 с/с).
По данным этой таблицы можно выявить целый ряд закономерностей:
- нуль и единица имеют единственное и одинаковое представление в любых системах счисления;
- основание системы счисления в любой системе имеет представление 10;
· незначащие нули слева от целой части и справа от дробной части числа не изменяют значений чисел;
| Таблица 14.1. Представление чисел в различных системах счисления | |||||||
| 10c/c | 2c/c | 8c/c | 16c/c | 10c/c | 2c/c | 8c/c | 16c/c |
| Целые числа | Целые числа | ||||||
| A | |||||||
| B | |||||||
| C | |||||||
| -1101 | D | ||||||
| E | |||||||
| F | |||||||
| и.т.д. | |||||||
| Дробные числа | Дробные числа | ||||||
| 0.5 | 0.1 | 0.4 | 0.8 | 0.0625 | 0.0001 | 0.04 | 0.1 |
| 0.25 | 0.01 | 0.2 | 0.4 | 0.03125 | 0.00001 | 0.02 | 0.08 |
| 0.125 | 0.001 | 0.1 | 0.2 | и т.д. |
- представление чисел в различных системах счисления допускает однозначное их преобразование из одной системы в другую.
В ЭВМ перевод из одной системы в другую осуществляется автоматически, по специальным программам. Правила перевода целых и дробных чисел отличаются.
Необходимо сделать несколько замечаний. В общем случае перевод любого числа с дробью из одной системы счисления в другую может привести к появлению иррациональных чисел, имеющих бесконечное количество разрядов в дробной части чисел. Естественно, что любое техническое устройство, например компьютер, может оперировать только с конечным числом цифр, являющихся старшими, наиболее значимыми разрядами.
Игнорирование, отбрасывание младших разрядов чисел приводит к их округлению. При этом разница между округляемым и полученным числами называется ошибкой округления. Следует учитывать, что округление результатов вычислений по любому неслучайному правилу приводит к ошибкам с ненулевым смещением [83].
 2014-02-17
2014-02-17 1208
1208
