Самостоятельная работа: Выпишите аналитический выражения функций 2-х переменных

Представление произвольной функции алгебры логики в виде формулы алгебры логики

Пусть F(х₁, х₂.....х _n) произвольная функция алгебры логики n переменных.

Рассмотрим формулу

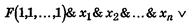
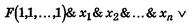
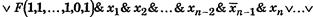
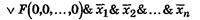
которая составлена следующим образом: каждое слагаемое этой логической суммы представляет собой конъюнкцию, в которой первый член является значением функции F при некоторых определенных значениях переменных х₁, х ₂,..., х _n, остальные же члены конъюнкции представляют собой переменные или их отрицания. При этом под знаком отрицания находятся те и только те переменные, которые в первом члене конъюнкции имеют значение 0. Вместе с тем формула содержит в виде логических слагаемых всевозможные конъюнкции указанноrо вида.

Ясно, что формула полностью определяет функцию F(х₁, х₂.....х _n). Иначе говоря, значения функции F и формулы совпадают на всех наборах значений переменных х₁, х₂.....х _n

Вид этой формулы может быть значительно упрощен. если в ней отбросить те логические слагаемые,

в которых первый член конъюнкции имеет значение 0 (и, следовательно. вся конъюнкция имеет значение 0). Если же в логическом слагаемом первый член конъюнкции имеет значение 1, то

, этот член конъюнкции можно не выписывать.

Таким образом, в результате получается формула, которая содержит только элементарные переменные высказывания и обладает следующими свойствами:

1) Каждое логическое слагаемое формулы содержит все переменные, входящие в функцию F(х₁, х₂.....х _n).

2) Все логические слагаемые формулы различны.

3) Ни одно логическое слагаемое формулы не содержит одновременно переменную и ее отрицание.

4) Ни одно логическое слагаемое формулы не содержит одну и ту же переменную дважды.

Перечисленные свойства будем называть свойствами совершенства или. коротко. свойствами (С)..