Активные RC-фильтры на основе операционных усилителей

Под электрическим фильтром понимается устройство, пропускающее колебания одних частот и задерживающее колебания других частот. На основе операционных усилителей и, как минимум, двух реактивных элементов (обычно конденсаторов) можно спроектировать устройства, имеющие свойства фильтров. Такие фильтры называются активными. Их наиболее эффективно можно использовать в диапазоне частот от нуля до единиц килогерц. В этом диапазоне частот невыгодно применять в качестве реактивных элементов индуктивности большого номинала, имеющие небольшую добротность и стабильность.

Область частот, пропускаемых фильтром, называется полосой пропускания. Область частот, задерживаемых фильтром, называется полосой задерживания. Между полосой пропускания и полосой задерживания лежит переходная область. В пределах полосы пропускания коэффициент передачи должен быть постоянен по модулю и равен некоторой величине с заданной точностью.

В пределах полосы задерживания коэффициент передачи не должен превосходить некоторого наперед заданного значения. Для переходной области определяющей характеристикой является ее крутизна. Чем она больше, тем меньше расстояние от полосы пропускания до полосы задерживания. В зависимости от типа частотной характеристики выделяют фильтры: нижних частот, верхних частот, полосовые. Это основные типы активных фильтров. Кроме того, существуют фильтры резонансного типа, полосно-задерживающие и режекторные, задерживающие сигнал на определенной частоте. По крутизне среза частотной характеристики в переходной области определяют порядок фильтра. Фильтром первого порядка называют фильтр с крутизной среза 20 децибелл на декаду. К таким фильтрам можно отнести рассмотренные ранее схемы интегратора и дифференциатора. Интегратор является фильтром нижних частот первого порядка, а дифференциатор- фильтром верхних частот первого порядка. Фильтры второго порядка имеют крутизну 40 децибелл на декаду, третьего- 60, четвертого - 80 и т.д.

Рассмотрим некоторые примеры типовых схем фильтров второго порядка на ОУ.

Фильтр нижних частот второго порядка (ФНЧ-2) на основе интегратора. Схема состоит из последовательно включенных цепи R1C1 и интегратора с элементами R2C2. Кроме того, в схеме действует общая обратная связь через резистор R3.

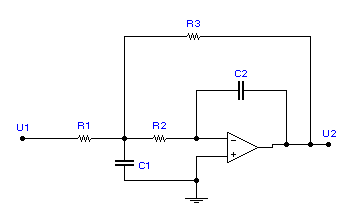
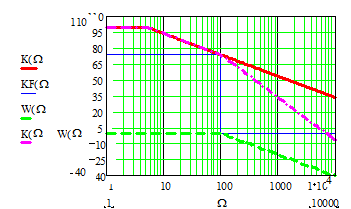
Покажем, как формируется результирующая ЛАЧХ схемы, с помощью ниже приведенного графика, на котором приведены по отдельности графики ЛАЧХ интегратора 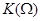, цепи R1C1 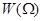, их суммы и характеристики 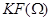, полученной за счет уменьшения общего коэффициента схемы с помощью цепи обратной связи через резистор R3. Из графиков видно, что результирующая ЛАЧХ характеризуется крутизной среза -40 децибелл на декаду, следовательно, соответствует ФНЧ-2, т.е. фильтру нижних частот 2-ого порядка. Точное выражение для частотной характеристики данной схемы можно получить, применяя метод суперпозиции и учитывая, что сигнал на выходе U2 определяется через сигнал на инвертирующем входе ОУ, также, как в случае ранее проведенного анализа инвертирующей схемы включения ОУ.

Соответствующая формула для данной схемы приводится к виду

.

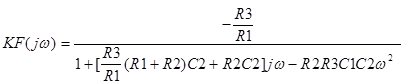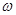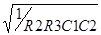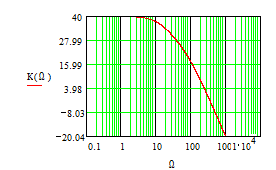
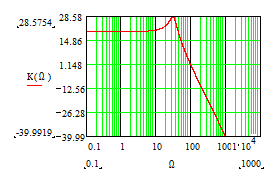
Из формулы можно определить, что частота ср=соответствует точке в переходной области, справа от которой крутизна делается равной -40 децибелл на декаду, т.к. в этой области частот поведение всей функции определяется последним слагаемым знаменателя. Этот член делается больше единицы и квадрат его величины определяет ход графика всей функции. Точный расчет по формуле позволяет получить графики ЛАЧХ для нескольких значений отношения 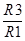, соответственно равных 100, 10 и 1. При расчете введена

нормированная частота .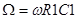

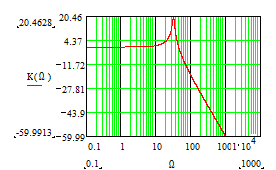
Из графиков видно, что в области частоты среза при увеличении глубины обратной связи появляется особенность в виде локального максимума. Частота этого максимума называется частотой полюса частотной характеристики фильтра, а величина характеризует добротность фильтра.

Фильтр верхних частот второго порядка на основе дифференциатора.

Схема такого фильтра получается из схемы на основе интегратора путем замены резисторов конденсаторами, а конденсаторов резисторами. Пример реализации такой схемы имеет вид

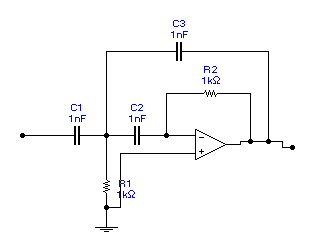
В днной схеме частота единичного усиления дифференциатора 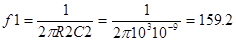килогерц

Частота среза цепи R1C1 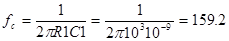кГц. Точная формула для расчета частотной характеристики имеет вид

.

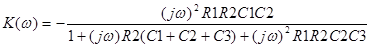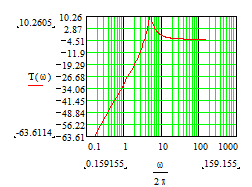
Результат расчета представлен в виде графика ЛАЧХ, на котором можно определить крутизну среза на линейном участке. Нетрудно убедиться, что она составляет 40 децибелл на декаду.

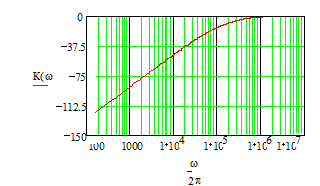
Кроме рассмотренных примеров схем активных фильтров второго порядка, в которых используется инвертирующий вход ОУ, возможно построение соответствующих схем с использованием неинвертирующего входа для подачи как напряжения сигнала, так и напряжения обратной связи. Примеры схем ФНЧ-2 и ФВЧ-2 на основе неинвертирующих усилителей напряжения и графики их ЛАЧХ приведены ниже.

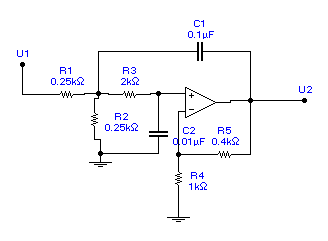
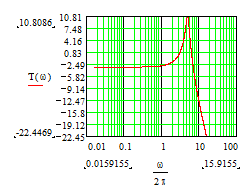
Этой схеме соответствует следующая расчетная формула для частотной характеристики:

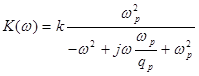, где , , , .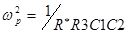

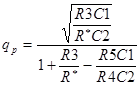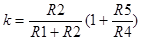Входящие в формулу коэффициенты определяют характерные особенности частотной характеристики схемы, а именно, при подстановке в формулу вместо текущей частоты ее значения, равного 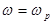, получаем для модуля 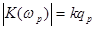, откуда следует, что коэффициент 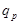, называемый добротностью, определяет величину максимума частотной характеристики на частоте полюса .

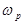На следующей схеме приведен пример реализации ФВЧ-2.

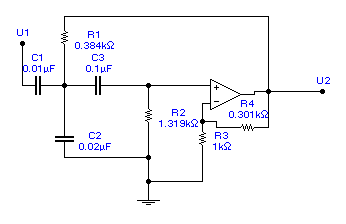
Для этой схемы расчетные формулы имеют вид:

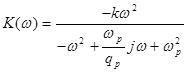, где ,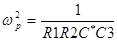

,

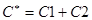
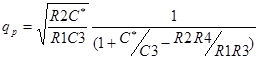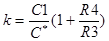
Путем каскадного соединения схем рассмотренных типов при варьировании параметрами их частотных характеристик можно создавать более сложные схемы, обеспечивающие выполнение практически любых заданных требований к их ЛАЧХ.