Зависимость расходов от среднедневной заработной платы

Район	Расходы на покупку продовольственных товаров в общих расходах, %, у	Среднедневная заработная плата одного работающего, руб., х
Нижегородская обл.	68,8	45,1
Кировская обл.	61,2	59,0
Владимирская обл.	59,9	57,2
Ивановская обл.	56,7	61,8
Самарская обл.	55,0	58,8
Ярославская обл.	54,3	47,2
Саратовская обл.	49,3	55,2

Требуется:

1. Для характеристики зависимости расходов на покупку продовольственных товаров (у) от среднедневной заработной платы одного работающего (х) рассчитать параметры следующих функций:

а) линейной;

б) степенной;

в) равносторонней гиперболы;

2. Оценить силу построенной зависимости.

3. Оценить качество каждой модели через среднюю ошибку аппроксимации А и коэффициент детерминации R².

4. Доказать статистическую значимость каждой модели по F -критерию Фишера и статистическую значимость найденных параметров по t – критерию Стьюдента.

5. По самой качественной модели спрогнозировать долю расходов на покупку продовольственных товаров, если среднедневная заработная плата одного работающего измениться до 50 руб и до 65 руб

Решение:

Построим корреляционное поле для исходных данных.

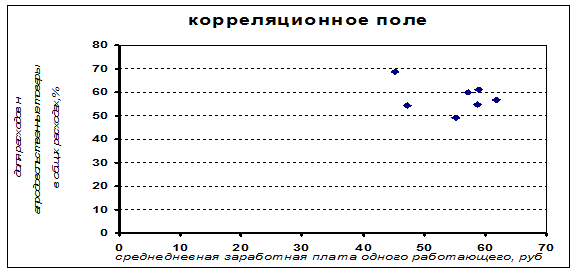
По расположению точек на корреляционном поле можно предположить, что зависимость между расходами на покупку продовольственных товаров и среднедневной заработной платы одного работающего нелинейная.

Линейная модель

Для расчета параметров а и b линейной регрессии y = a+ b x решаем систему уравнений (2.6) относительно а и b:

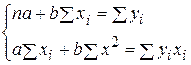
По исходным данным рассчитываем: 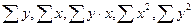и заполняем в расчетной таблице первые шесть столбцов (табл. 4.2.2).

Таблица 4.2.2

Расчетная таблица для линейной модели

№	y	x	yx	x2	y2	(y-)2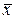	(х-)2	ŷx	y-ŷx	(y-ŷx)2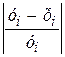
	68,8	45,1	3102,88	2034,01	4733,44	119,12	96,04	61,28	7,52	56,61	0,11
	61,2	59,0	3610,80	3481,00	3745,44	10,98	16,81	56,47	4,73	22,40	0,08
	59,9	57,2	3426,28	3271,84	3588,01	4,06	5,29	57,09	2,81	7,90	0,05
	56,7	61,8	3504,06	3819,24	3214,89	1,41	47,61	55,50	1,20	1,44	0,02
	55,0	58,8	3234,00	3457,44	3025,00	8,33	15,21	56,54	-1,54	2,36	0,03
	54,3	47,2	2562,96	2227,84	2948,49	12,86	59,29	60,55	-6,25	39,05	0,12
	49,3	55,2	2721,36	3047,04	2430,49	73,71	0,09	57,78	-8,48	71,94	0,17
Σ	405,2	384,4	22162,34	21338,41	23685,76	230,47	240,34	405,2	0,0	201,71	0,57
Ср. зн-е	57,89	54,90	3166,05	3048,34	3383,68	-		-

Для данных характеристик получаем следующую систему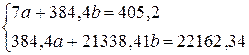

Решение этой системы находим методом Крамера, в результате чего получаем а =76,88 и b =-0,35

Тогда уравнение регрессии, описывающее зависимость между расходами на покупку продовольственных товаров и среднедневной заработной платы одного работающего имеет следующий вид: ŷ = 76,88 - 0,35 х.

Таким образом при увеличением среднедневной заработной платы одного работающего на 1 руб. доля расходов на покупку продовольственных товаров снижается в среднем на 0,35% в общей доле расходов.

Рассчитаем коэффициент корреляции, чтобы увидеть тесноту линейной связи между среднедневной заработной платы одного работающего и расходами на покупку продовольственных товаров:

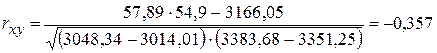
По результату делаем вывод, что линейная связь между среднедневной заработной платы одного работающего и расходами на покупку продовольственных товаров умеренная и обратная.

Качество модели определим через значение коэффициента детерминации. Для этого в расчетной таблице заполним столбцы с 7 по 11

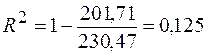
Полученный результат доказывает, что качество построенной линейной модели низкое. Такую модель нельзя использовать для построения прогноза и дальнейшего анализа среднедневной заработной платы одного работающего и расходов на покупку продовольственных товаров.

Найдем величину средней ошибки аппроксимации А:

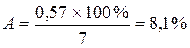
В среднем, расчетные значения отклоняются от фактических на 8,1%, что допускается.

Проверим статистическую значимость полученного линейного уравнения регрессии, для этого найдем расчетное значение F -критерия Фишера:

F _расч=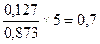

Сравним фактическое (расчетное) значение критерия F_расч с табличным значением F _табл. F _табл (α= 0,05; ν₁= 1; ν₂= 5 )= 6,61

Так как F_расч < F _табл при заданном уровне значимости α=0,05, гипотеза H₀ о случайной природе формирования уравнения регрессии не отклоняется и признается статистическая незначимость и ненадежность полученного линейного уравнения регрессии.

Для оценки статистической значимости параметров регрессии воспользуемся t – критерием Стьюдента. Найдем расчетное значение t – критерии для каждого параметра.

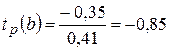
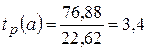
Полученные расчетные значения сравниваем с табличным t _табл (α =0,05; ν=5)=2,571

Так как 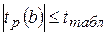, то гипотеза H₀ о статистической незначимости параметра b принимается. То есть параметр b в полученном уравнении регрессии можно считать равным 0. Можно говорить о том, что расходы на покупку продовольственных товаров не зависят (по линейному закону) от среднедневной заработной платы одного работающего.

Прогноз по этой модели делать не имеет смысла, потому что по всем критериям модель признана несостоятельной.

Степенная модель

Для построения степенной модели y=a·x ^b нужно провести линеаризацию переменных. Для степенной модели необходимо рассчитать у ^*=ln y и x ^*=ln x

Для расчетов будем использовать данные из таблицы 4.2.3.

Таблица 4.2.3

Расчетная таблица для степенной модели

№	Y*	X*	Y*X*	Y*2	X*2	ŷx	y-ŷx	(y-ŷx)2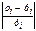
	4,23	3,81	16,12	17,90	14,51	60,98	7,82	61,15	0,113663
	4,11	4,08	16,78	16,93	16,63	56,28	4,92	24,19	0,080361
	4,09	4,05	16,56	16,75	16,37	56,80	3,10	9,58	0,051674
	4,04	4,12	16,65	16,30	17,01	55,51	1,19	1,42	0,021014
	4,01	4,07	16,33	16,06	16,60	56,34	-1,34	1,79	0,024345
	3,99	3,85	15,40	15,96	14,86	60,16	-5,86	34,31	0,10787
	3,90	4,01	15,63	15,19	16,09	57,41	-8,11	65,79	0,164529
Σ	28,38	28,00	113,46	115,09	112,06	403,48	1,72	198,23	0,56
Ср. зн-е	4,05	4,00	16,21	16,44	16,01	-	-	-

Для новых данных получаем следующую систему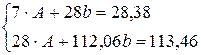

Решение этой системы находим методом Крамера, в результате чего получаем А =5,247197 и b =-0,29842

Получим линейное уравнение: Ŷ* = 5,247197 – 0,29842· х*.

Необходимо вернуться к параметрам искомого степенного уравнения (А =).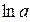

ŷ=е^5,247192∙ x ^-0,29842 =190,0319· x ^-0,29842.

Подставляя в данное уравнение фактические значения х, получаем теоретические значения результата ŷ_x (заполняем 7, 8 и 9 столбцы расчетной таблицы).

По ним рассчитаем показатели тесноты связи (индекс корреляции ρ_ху ) и среднюю ошибку аппроксимации А:

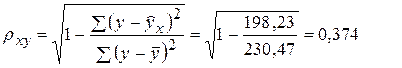
Характеристики степенной модели показывают, что она несколько лучше описывает взаимосвязь между среднедневной заработной платы одного работающего и расходами на покупку продовольственных товаров, чем линейная функция.

Найдем величину средней ошибки аппроксимации А:

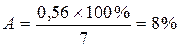
В среднем, расчетные значения отклоняются от фактических на 8%, что является нормой.

Проверим статистическую значимость полученного степенного уравнения регрессии, для этого найдем расчетное значение F -критерия Фишера:

F _расч=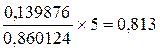

Сравним фактическое (расчетное) значение критерия F_расч с табличным значением F _табл. F _табл (α= 0,05; ν₁= 1; ν₂= 5 )= 6,61

Так как F_расч < F _табл при заданном уровне значимости α=0,05, гипотеза H₀ о случайной природе формирования уравнения регрессии не отклоняется и признается статистическая незначимость и ненадежность полученного степенного уравнения регрессии.

Для оценки статистической значимости параметров регрессии воспользуемся t – критерием Стьюдента. Найдем расчетное значение t – критерии для каждого параметра.

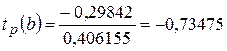
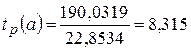
Полученные расчетные значения сравниваем с табличным t _табл (α =0,05; ν=5)=2,571

Так как 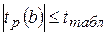, то гипотеза H₀ о статистической незначимости параметра b принимается. То есть параметр b в полученном уравнении регрессии можно считать равным 0. Можно говорить о том, что расходы на покупку продовольственных товаров не зависят (по степенному закону) от среднедневной заработной платы одного работающего.

Прогноз по этой модели делать не имеет смысла, потому что по всем критериям модель признана несостоятельной.

Гиперболическая модель

Для построения гиперболической модели y=a + b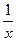 нужно провести линеаризацию переменных, которая заключается в следующем преобразовании: x ^*=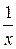

Для расчетов будем использовать данные из таблицы 4.2.4.

Таблица 4.2.4

Расчетная таблица для гиперболической модели

№	у	X*	уX*	y2	X*2	ŷx	y-ŷx	(y-ŷx)2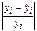
	68,8	0,022173	1,525499	4733,44	0,000492	61,82048	6,98	48,71373	0,101447
	61,2	0,016949	1,037288	3745,44	0,000287	56,3111	4,89	23,90137	0,079884
	59,9	0,017483	1,047203	3588,01	0,000306	56,87362	3,03	9,158969	0,050524
	56,7	0,016181	0,917476	3214,89	0,000262	55,50119	1,20	1,43714	0,021143
	55,0	0,017007	0,935374	3025,00	0,000289	56,3719	-1,37	1,882107	0,024944
	54,3	0,021186	1,150424	2948,49	0,000449	60,78004	-6,48	41,99088	0,119338
	49,3	0,018116	0,893116	2430,49	0,000328	57,54167	-8,24	67,92521	0,167174
Σ	405,2	0,129095	7,506379	23685,76	0,002413	405,20		195,0094	0,564453
Ср. зн-е	57,89	0,018442	1,07234	3383,68	0,000345	-	-	-

Для новых данных получаем следующую систему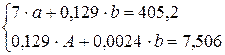

Решение этой системы находим методом Крамера, в результате чего получаем а =38,43534 и b =1054,67

Получим линейное уравнение: 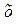= 38,43534+1054,67· х*.

Необходимо вернуться к исходному виду искомого гиперболического уравнения.

.

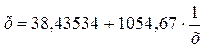Подставляя в данное уравнение фактические значения х, получаем теоретические значения результата ŷ_x (заполняем 7, 8 и 9 столбцы расчетной таблицы).

По ним рассчитаем показатели тесноты связи (индекс корреляции ρ_ху ) и среднюю ошибку аппроксимации А:

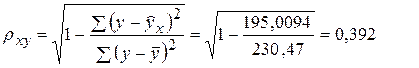
Характеристика гиперболической модели показывает, что она несколько лучше описывает взаимосвязь между среднедневной заработной платы одного работающего и расходами на покупку продовольственных товаров, чем линейная и степенная функции.

Найдем величину средней ошибки аппроксимации А:

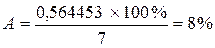
В среднем, расчетные значения отклоняются от фактических на 8%, что является нормой.

По критерию Фишера модель статистически незначима, по критерию Стьюдента параметр b статистически не значим.

Из всех предложенных моделей гиперболическая является наилучшей, но назвать ее качественной нельзя. То есть на практике делать прогноз по этой модели нет смысла. Рассмотрим чисто формально, как делается прогноз, по предложенной модели. Подставляем в модель то значение независимой переменной, для которого необходимо сделать прогноз.

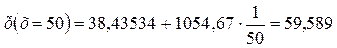
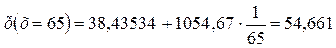
Множественная регрессия

Специфика уравнения множественной регрессии

Зачастую на практике значения экономических переменных определяются влиянием не одного, а нескольких факторов. Например, рассматривая уровень фондоотдачи на различных предприятиях одной отрасли, мы можем установить, что величина его зависит от размеров предприятия, удельного веса активной части фондов, степени изношенности фондов, их обновления и ряда других факторов; урожайность зависит от количества внесенных удобрений, сроков уборки, количества осадков; вес человека – от его роста, объема груди и т.п.

Таким образом, модель множественной регрессии – это модель зависимости результирующей переменной более чем от одной независимой переменной.

Выше была рассмотрена зависимость между двумя признаками, т.е. речь шла о так называемой парной корреляции. На практике же чаще изменение рассматриваемого признака зависит от нескольких причин. В таких случаях изучение корреляционной связи не может ограничиться парными зависимостями, и в анализ необходимо включить другие признаки-факторы, существенно влияющие на изучаемую зависимую переменную.

Наиболее широкое применение получили следующие методы построения уравнения множественной регрессии:

-метод исключения;

-метод включения;

-шаговый регрессионный анализ.

Каждый из этих методов по-своему решает проблему отбора факторов, давая в целом близкие результаты - отсев факторов из полного его набора (метод исключения), дополнительное введе­ние фактора (метод включения), исключение ранее введенного фактора (шаговый регрессионный анализ).

Этап спецификации (3этап) модели множественной регрессии включает несколько этапов:

1) отбор фактор, которые окончательно войдут в модель;

2) выбор формы связи (уравнения регрессии);

3) обеспечение достаточного объема совокупности для получения несмещенных оценок.

Включение в уравнение множественной регрессии того или иного набора факторов связано прежде всего с представлением исследователя о природе взаимосвязи моделируемого показателя с другими экономическими явлениями. Факторы, включаемые во множественную регрессию, должны отвечать следующим требова­ниям

1. Они должны быть количественно измеримы. Но очень часто возникает необходимость включить показатель, имеющий качественную характеристику. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность (например, в модели стоимости объектов недвижимости учитывается место нахождения недвижимости: районы могут быть проранжированы). Как это происходит мы рассмотрим позднее (смотри тему 6).

2. Факторы включаемые в модель не должны находиться в точной функциональной зависимости между собой. Если между факторами существует высокая корреляция, то нельзя определить их изолированное влияние на результативный показатель и параметры уравнения регрессии оказываются не интерпретируемыми. Считается, что факторы x_i и x_j находятся в точной функциональной зависимости между собой, если 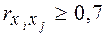. Такие факторы дублируют друг друга в модели, и один из них не должен войти в модель, то есть подвержен исключению из модели.

Насыщение модели лишними факторами не только не снижает величину остаточной дисперсии и не увеличивает показатель детерминации, но и приводит к статистической незначимости параметров регрессии по t -критерию Стьюдента.

Таким образом, хотя теоретически регрессионная модель позволяет учесть любое число факторов, практически в этом нет необходимости. Отбор факторов производится на основе качественного теоретико-экономического анализа. Однако теоретический анализ часто не позволяет однозначно ответить на вопрос о количественной взаимосвязи рассматриваемых признаков и целесообразности включения фактора в модель. Поэтому отбор факторов обычно осуществляется в две стадии: на первой подбираются факторы исходя из сущности проблемы; на второй – на основе матрицы парных коэффициентов корреляции определяются дублирующие факторы.

Предпочтение при этом отдается не фактору, более тесно связанному с результатом, а тому фактору, который при достаточно тесной, связи с результатом имеет наименьшую тесноту связи с другими факторами. В этом требовании проявляется специфика множественной регрессии как метода исследования комплексного воздействия факторов в условиях их независимости друг от друга.

Например, при изучении зависимости у=f(x,w,z) матрица парных коэффициентов корреляции оказалась следующей:

	y	x	w	z
y
x	0,8
w	-0,7	0,8
z	0,7	-0,6	0,2

Очевидно, что факторы х и w дублируют друг друга. В модель целесообразно включить фактор w, а не х, так как корреляция z с результатом у и корреляция фактора х с у сильные, но зато слабее межфакторная корреляция w c z, чем x c z. Поэтому в данном случае в уравнение множественной регрессии включаются факторы w, z.

На первый взгляд может показаться, что матрица парных ко­эффициентов корреляции играет главную роль в отборе факто­ров. Вместе с тем вследствие взаимодействия факторов парные коэффициенты корреляции не могут в полной мере решать во­прос о целесообразности включения в модель того или иного; фактора. Эту роль выполняют показатели частной корреляции, оценивающие в чистом виде тесноту связи фактора с результа­том. Матрица частных коэффициентов корреляции наиболее широко используется в процедуре отсева факторов. При отборе факторов рекомендуется пользоваться следующим правилом; число включаемых факторов обычно в 6—7 раз меньше объема совокупности, по которой строится регрессия. Если это соотно­шение нарушено, то число степеней свободы остаточной вариа­ции очень мало. Это приводит к тому, что параметры уравнения регрессии оказываются статистически незначимыми, а F -критерий меньше табличного значения.

Оценка параметров уравнения множественной линейной регрессии

Уравнение линейной множественной регрессии имеет вид:

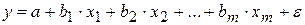(5.3)

где у – теоретические значения результативного признака, полученные подстановкой соответствующих значений факторных признаков в уравнение ре­грессии;

x₁ ,x₂...,x_m – факторные признаки;

b₁, b₂,..., b_m – параметры модели (коэффициенты регрессии).

Параметры уравнения могут быть определены методом наименьших квадратов, который минимизирует выражение:

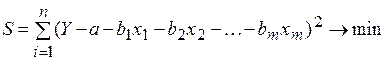(5.4)

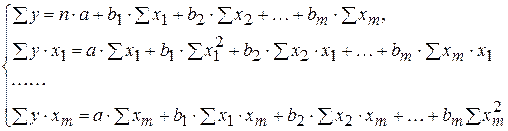(5.5)

Ее решение может быть осуществлено методом определителей:

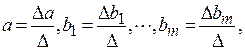
где 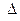– определитель системы;

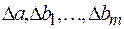– частные определители.

При этом

,

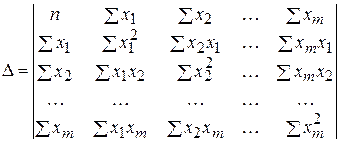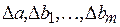получаются путем замены соответствующего столбца матрицы определителя системы данными левой части системы.

Параметры b₁, b₂,..., b_m характеризуют среднее изменение результата у с изменением соот­ветствующего фактора на единицу при неизмененном значении других факторов, закрепленных на среднем уровне.

Возможен и иной подход к определению параметров множе­ственной регрессии, когда на основе матрицы парных коэффи­циентов корреляции строится уравнение регрессии в стандарти­зованном масштабе:

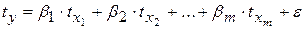(5.6)

где 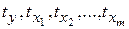- стандартизованные переменные;

β_j – стандартизованные параметры регрессии.

Применяя МНК к уравнению множественной регрессии в стандартизованном масштабе, после соответствующих преобра­зований получим.систему нормальных уравнений вида:

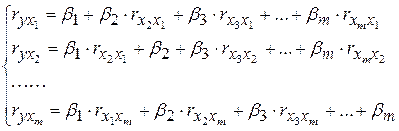(5.7)

Решая ее методом определителей, найдем параметры - стан­дартизованные коэффициенты регрессии (β-коэффициенты).

Стандартизованные коэффициенты регрессии показывают на сколько сигм изменится в среднем результат, если соответствующий фактор х_i изменится на одну сигму при неизменном среднем уровне других факторов. В силу того, что все перемен­ные заданы как центрированные и нормированные, стандартизованные коэффициенты регрессии β_i сравнимы между coбой. Сравнивая их друг с другом, можно ранжировать факторы по силе их воздействия на результат. В этом основное достоинстве стандартизованных коэффициентов регрессии в отличие от коэффициентов «чистой» регрессии, которые несравнимы между собой.

Например, пусть функция издержек производства у (тыс. руб. характеризуется уравнением вида

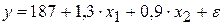
где х₁ – основные производственные фонды (тыс.руб.);

х₂ – численность занятых в производстве (чел.).

Анализируя его, мы видим, что при той же занятости допол­нительный рост стоимости основных производственных фондов на 1 тыс. руб. влечет за собой увеличение затрат в среднем на 1,3 тыс. руб., а увеличение численности занятых на одного человека способствует при той же технической оснащенности предприя­тий росту затрат в среднем на 0,9 тыс. руб. Однако это не означа­ет, что фактор х₁ оказывает более сильное влияние на издержки производства по сравнению с фактором х₂. Такое сравнение воз­можно, если обратиться к уравнению регрессии в стандартизо­ванном масштабе. Предположим, оно выглядит так:

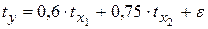
Это означает, что с ростом фактора х₁ на одну сигму при не­изменной численности занятых затраты на продукцию увеличи­ваются в среднем на 0,6 сигмы. Так как β₁ < β₂ (0,6 < 0,75), то мож­но заключить, что большее влияние оказывает на производство продукции фактор х₂, а не х₁, как кажется из уравнения регрессии в натуральном масштабе.

В парной зависимости стандартизованный коэффициент рег­рессии есть не что иное, как линейный коэффициент корреляции r_yx. Подобно тому, как в парной зависимости коэффициенты рег­рессии и корреляции связаны между собой, так и во множествен­ной регрессии коэффициенты «чистой» регрессии b_j связаны со стандартизованными коэффициентами регрессии β_j, а именно:

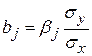(5.8)

где σ_у – среднее квадратическое отклонение у,

σ_х – среднее квадратическое отклонение х.

Параметр а определяется как

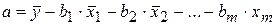(5.9)

Рассмотренный смысл стандартизованных коэффициентов регрессии позволяет их использовать при отсеве факторов – из модели исключаются факторы с наименьшим значением β_j.

Фиктивные и нефиктивные переменные

В регрессионных моделях в качестве объясняющих пере­менных часто приходится использовать не только количествен­ные (определяемые численно), но и качественные переменные. Например, спрос на некоторое благо может определяться ценой данного блага, ценой на заменители данного блага, ценой до­полняющих благ, доходом потребителей и т.д. (эти показатели определяются количественно). Но спрос может также зависеть от вкусов потребителей, их ожиданий, национальных и религи­озных особенностей и т.д. А эти показатели представить в чис­ленном виде нельзя. Возникает проблема отражения в модели влияния таких переменных на исследуемую величину. Чтобы ввести такие переменные в регрессионную модель, им должны быть присвоены те или иные цифровые метки, то есть качественные переменные преобразованы в количественные. Такого рода сконструированные переменные в эконометрике называют фиктивными.

Обычно в моделях влияние качественного фактора выражается в виде фиктивной (искусственной) переменной, которая отражает два противоположных состояния качественного фак­тора. Например, «фактор действует» — «фактор не действует», «курс валюты фиксированный» — «курс валюты плавающий»,, «сезон летний» — «сезон зимний» и т.д. В этом случае фиктивная переменная может выражаться в двоичной форме:

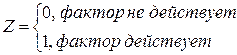(6.1)

Например, Z = О, если потребитель не имеет высшего образования, Z = 1, если потребитель имеет высшее образование; Z = 0, если в обществе имеются инфляционные ожидания, Z = 1, если инфляционных ожиданий нет.

Регрессионные модели, содержащие лишь качественные объясняющие переменные, называются ANOVА-моделями (моделями дисперсионного анализа).

Например, пусть у – начальная заработная плата сотрудника.

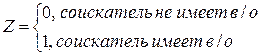
Тогда зависимость можно выразить моделью парной регрессии

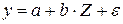
тогда,

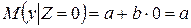
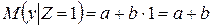
При этом коэффициент а определяет среднюю начальную заработную плату при отсутствии высшего образования. Коэффициент b указывает, на какую величину отличаются средние начальные заработные платы при наличии и при отсутствии высшего образования у претендента. Проверяя статистическую значимость коэффициента b с помощью t -статистики либо значимость коэффициента детерминации R² с помощью F -статистики, можно определить, влияет или нет наличие высшего образования на начальную заработную плату.

Нетрудно заметить, что ANOVA-модели представляют собой кусочно-постоянные функции. Однако такие модели в экономике крайне редки. Гораздо чаще встречаются модели, содержащие как качественные, так и количественные переменные

Пример 2. Анализируется объем S сбережений домохозяйства за 11 лет. Предполагается, что его размер s_t в текущем году t зависит от величины y_t-1 располагаемого дохода Y в предыдущем году и от величины z_t реальной процентной ставки Z в текущем году. Статистические данные представлены в таблице 7.5.1:

Таблица 7.5.1