n.1. Формула Тейлора для многочлена.
Глава 1 Рассмотрим некоторый многочлен степени 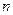 с вещественными коэффициентами:
с вещественными коэффициентами:
Глава 2 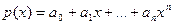 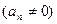 | Глава 3 (1) |
Зададим произвольное вещественное число  и в правой части равенства (1) представим
и в правой части равенства (1) представим 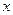 в виде
в виде 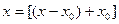 :
:
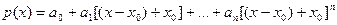
Раскрыв здесь квадратные скобки и приведя подобные члены при одинаковых степенях 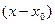 , в результате получим разложение многочлена (1) по степеням
, в результате получим разложение многочлена (1) по степеням 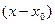 :
:
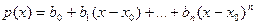 , , | (2) |
где 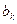
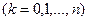 - постоянные, зависящие от исходных коэффициентов и от числа
- постоянные, зависящие от исходных коэффициентов и от числа 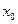 .
.
При больших 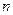 , на практике, указанный выше способ разложения многочлена по степеням
, на практике, указанный выше способ разложения многочлена по степеням 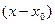 весьма трудоемок. Оказывается, имеется простой способ отыскания коэффициентов
весьма трудоемок. Оказывается, имеется простой способ отыскания коэффициентов 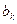
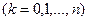 разложения многочлена по степеням
разложения многочлена по степеням 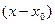 . Будем последовательно дифференцировать равенство (2):
. Будем последовательно дифференцировать равенство (2):
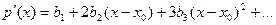
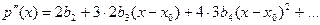
................................
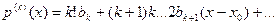
................................
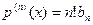 .
.
Полагая в каждом из этих равенств 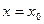 получим
получим
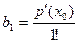
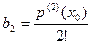
.........
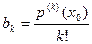
.........
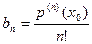
Если кроме того положить 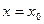 в (2), то считая, как обычно,
в (2), то считая, как обычно, 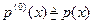 и
и 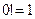 будем также иметь
будем также иметь
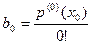
Таким образом, для коэффициентов разложения (2) многочлена по степеням имеем следующие формулы
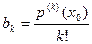 , , 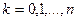 | (3) |
В итоге заключаем, что разложение (2) можно записать в виде (4):
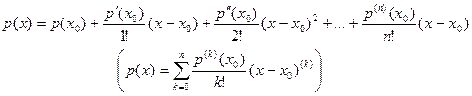 | (4) |
Формула (4) называется формулой Тейлора по степеням 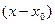 для многочлена
для многочлена 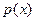 степени
степени 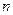 . Из вывода этой формулы следует, что разложение многочлена по степеням
. Из вывода этой формулы следует, что разложение многочлена по степеням 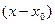 является единственным, так как коэффициенты любого такого разложения однозначно определяются по формулам (3).
является единственным, так как коэффициенты любого такого разложения однозначно определяются по формулам (3).
Формулу Тейлора по степеням 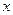 для многочлена
для многочлена 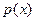 , то есть формулу
, то есть формулу
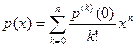
называют также формулой Маклорена.
n.2. Локальная формула Тейлора.
Пусть функция 
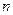 раз дифференцируема в точке
раз дифференцируема в точке  . Напомним, это означает, что существует такая окрестность
. Напомним, это означает, что существует такая окрестность 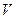 точки
точки  , в которой определена сама функция
, в которой определена сама функция  и существуют конечные производные
и существуют конечные производные
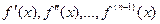
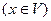
при этом в точке  существует также конечная производная
существует также конечная производная 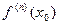 . Поэтому, в частности, определен многочлен
. Поэтому, в частности, определен многочлен
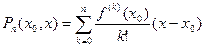 ,
,
называемый (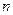 -ым) многочленом Тейлора функции
-ым) многочленом Тейлора функции  в точке
в точке  .
.
Положим
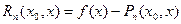
Тогда
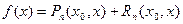
Эта формула или, в более явном виде, формула
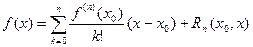 | (1) |
называется формулой Тейлора функции в точке  , а функция
, а функция 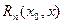 - остаточным членом формулы Тейлора.
- остаточным членом формулы Тейлора.
Ниже будет доказано, что остаточный член формулы Тейлора может быть записан в виде
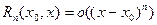 (при (при 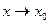 ) ) | (2) |
Остаточный член в такой форме обычно называют остаточным членом в форме Пеано, а формулу Тейлора с остаточным членом в такой форме, т. е. формулу
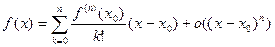 | (3) |
называют, соответственно, формулой Тейлора с остаточным членом в форме Пеано или, также, локальной формулой Тейлора.
Лемма 1. Пусть функция 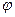
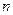 раз дифференцируема в точке
раз дифференцируема в точке  и
и
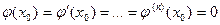 . . | (4) |
Тогда
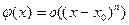 . . | (5) |
Д о к а з а т е л ь с т в о. Докажем утверждение леммы по индукции.
При 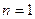 в силу дифференцируемости функции
в силу дифференцируемости функции 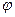 в точке
в точке  имеем
имеем
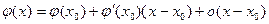
А так как по условию (4)
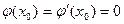 ,
,
то это означает, что
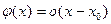
таким образом, при 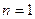 утверждение леммы справедливо.
утверждение леммы справедливо.
Предположим, что оно справедливо при 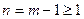 , и покажем, что тогда оно справедливо и при
, и покажем, что тогда оно справедливо и при 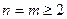 .
.
Действительно, поскольку 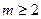 , то функция
, то функция 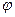 имеет в некоторой окрестности
имеет в некоторой окрестности 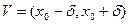 производную
производную 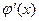 , и по условию (4) (для
, и по условию (4) (для 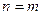 )
)
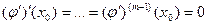
Тогда по индукционному предположению
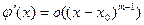 | (6) |
Далее, так как функция 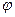
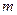 раз дифференцируема в точке
раз дифференцируема в точке  и
и 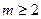 , то для любой точки
, то для любой точки 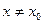 из окрестности
из окрестности 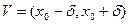 , в которой существует конечные производные
, в которой существует конечные производные
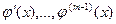 ,
,
Имеет место и формула конечных приращений Лагранжа
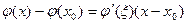 , , | (7) |
где точка 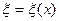 лежит между точками
лежит между точками 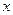 и
и  . (Рекомендуется проверить, что на отрезке с концами в точках
. (Рекомендуется проверить, что на отрезке с концами в точках 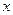 и
и  функция удовлетворяет всем условиям теоремы Лагранжа).
функция удовлетворяет всем условиям теоремы Лагранжа).
Поскольку по условию 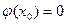 , то из формул (6) и (7) следует, что
, то из формул (6) и (7) следует, что
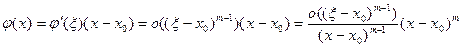
Полагая здесь
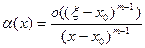
будем иметь
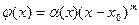
Поэтому равенство (5) при 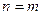 будет доказано, если будет показано, что
будет доказано, если будет показано, что
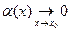 | (8) |
Действительно, так как точка 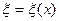 лежит между точками
лежит между точками 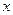 и
и  , то
, то
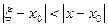 | (9) |
и, следовательно,
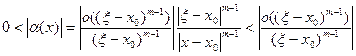 | (10) |
Остаётся заметить, что в силу (8) 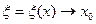 при
при 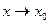 и, значит,
и, значит,
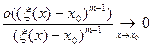
Тогда по принципу двух милиционеров из (10) следует (8)
Теорема 1. Если функция 
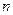 раз дифференцируема в точке
раз дифференцируема в точке  , то для нее имеет место формула Тейлора с остаточным членом в форме Пеано (3).
, то для нее имеет место формула Тейлора с остаточным членом в форме Пеано (3).
Д о к а з а т е л ь с т в о. Достаточно заметить, что при выполнении условий теоремы функция
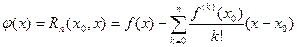
Удовлетворяет условиям леммы 1
Замечание 1. Вот другая, равносильная формулировка теоремы 1: Если функция  имеет в точке
имеет в точке  конечные производные до порядка
конечные производные до порядка 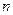 включительно, то для нее имеет место локальная формула Тейлора (3).
включительно, то для нее имеет место локальная формула Тейлора (3).
nо3. Формула Тейлора с остаточным членом в форме Коши и в форме Лагранжа.
Теорема 2. Пусть на отрезке 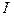 с концами в точках
с концами в точках  и
и 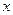 функция
функция  и все ее производные до порядка
и все ее производные до порядка 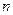 включительно являются непрерывными функциями, а во внутренних точках этого отрезка существует конечная производная
включительно являются непрерывными функциями, а во внутренних точках этого отрезка существует конечная производная 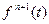 . Тогда, для любой непрерывной на этом отрезке функции
. Тогда, для любой непрерывной на этом отрезке функции 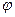 , дифференцируемой во внутренних точках этого отрезка и имеющей в каждой из этих точек отличную от нуля производную, существует точка
, дифференцируемой во внутренних точках этого отрезка и имеющей в каждой из этих точек отличную от нуля производную, существует точка 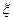 , лежащая между точками
, лежащая между точками 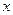 и
и  , такая, что остаточный член в формуле Тейлора может быть записан в виде
, такая, что остаточный член в формуле Тейлора может быть записан в виде
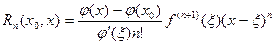 . . | (1) |
Д о к а з а т е л ь с т в о. На отрезке 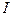 с концами в точках
с концами в точках  и
и 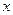 рассмотрим функцию переменной
рассмотрим функцию переменной 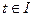 :
:
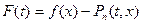 ,
,
где
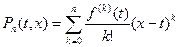
 .
.
Из условий теоремы и определения функции 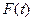 следует, что она непрерывна на отрезке
следует, что она непрерывна на отрезке 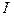 и дифференцируема во внутренних точках этого отрезка. По условию теоремы функция
и дифференцируема во внутренних точках этого отрезка. По условию теоремы функция 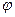 обладает теми же свойствами.
обладает теми же свойствами.
Таким образом, функции 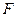 и
и 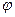 на отрезке I удовлетворяют всем условиям теоремы Коши о среднем значении для дифференцируемых функций.
на отрезке I удовлетворяют всем условиям теоремы Коши о среднем значении для дифференцируемых функций.
По этой теореме между точками  и
и 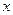 найдется такая точка
найдется такая точка 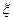 , что
, что
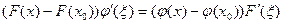 | (2) |
Поскольку
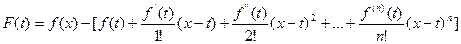 , , | (3) |
то нетрудно видеть, что
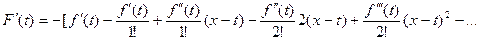 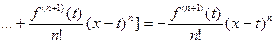 . . | (4) |
К тому же, как следует из (3),
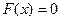 | (5) |
и
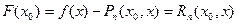 | (6) |
Из формулы (2), (4) – (6) имеем
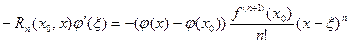
В свою очередь отсюда, с учетом того, что по условию теоремы 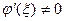
(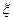 - внутренняя точка отрезка
- внутренняя точка отрезка 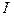 ), получим искомое равенство (1).
), получим искомое равенство (1).
Следствие. Если на отрезке с концами в точках  и
и 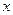 функция
функция  и все ее производные до порядка
и все ее производные до порядка 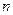 включительно являются непрерывными функциями, а во внутренних точках этого отрезка существует конечная производная
включительно являются непрерывными функциями, а во внутренних точках этого отрезка существует конечная производная 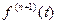 , то остаточный член в формуле Тейлора
, то остаточный член в формуле Тейлора
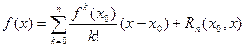 | (7) |
может быть записан, как в форме Коши:
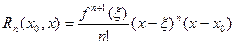 , , | (8) |
так и в форме Лагранжа:
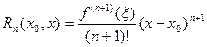 | (9) |
(здесь 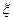 лежит между точками
лежит между точками 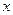 и
и  , при этом является, вообще говоря, разной в формулах (8) и (9)).
, при этом является, вообще говоря, разной в формулах (8) и (9)).
Д о к а з а т е л ь с т в о. Формула (8) вытекает из формулы (1), если в ней положить
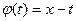
В свою очередь, формула (9) вытекает из той же формулы (1), если в последней положить
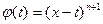
Таким образом, если выполнены условия следствия из теоремы 2, то формулу Тейлора для функции  можно записать как в виде
можно записать как в виде
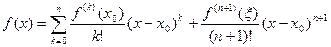 | (10) |
(формула Тейлора с остаточным членов в форме Лагранжа),
так и в виде
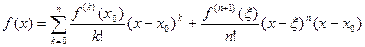 | (11) |
(формула Тейлора с остаточным членом в форме Коши).
nо4. Разложение некоторых элементарных функцией по формуле Тейлора.
Если 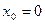 , то формула Тейлора функции
, то формула Тейлора функции  имеет особенно простой вид:
имеет особенно простой вид:
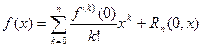 | (1) |
В этом случае она называется формулой Маклорена. Остаточный член в ней в форме Пеано, Лагранжа и Коши, соответственно, имеет вид
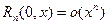 ,
,
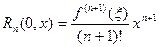 ,
,
и
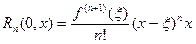
Укажем разложения некоторых элементарных функций по формуле Маклорена.
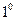 . Пусть
. Пусть 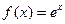 . Эта функция имеет производные любого порядка и в любой точке
. Эта функция имеет производные любого порядка и в любой точке 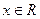 (в таких случаях говорят, что функция бесконечно дифференцируема
(в таких случаях говорят, что функция бесконечно дифференцируема 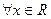 ).
).
Как известно
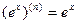
Поэтому формула Маклорена функции 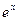 имеет вид (
имеет вид (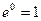 ):
):
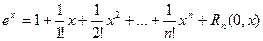
где остаточный член можно записать в любой из форм:
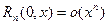 (в форме Пеано)
(в форме Пеано)
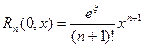 (в форме Лагранжа)
(в форме Лагранжа)
и
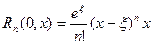 (в форме Коши),
(в форме Коши),
где точка 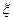 в каждой из двух последних формул лежит между точками
в каждой из двух последних формул лежит между точками 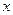 и
и 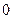 .
.
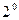 . Пусть
. Пусть 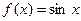 . Так как эта функция бесконечно дифференцируема на всей вещественной оси и
. Так как эта функция бесконечно дифференцируема на всей вещественной оси и
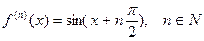 ,
,
то
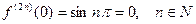 ;
;
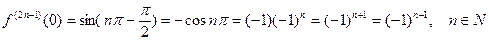
и, следовательно,
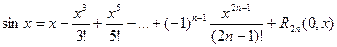
При этом остаточный член в форме Пеано имеет вид:
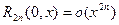 ,
,
соответственно остаточный член в форме Лагранжа выглядит следующим образом:
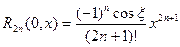 | (2) |
а остаточный член в форме Коши имеет вид:
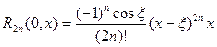 | (3) |
Замечание 1. Для доказательства, например, равенства (2) достаточно заметить, что остаточный член 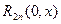 в форме Лагранжа в общем случае имеет вид:
в форме Лагранжа в общем случае имеет вид:
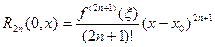
а затем убедиться в том, что для функции 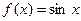 имеют место равенства
имеют место равенства
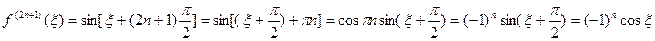
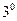 . Пусть
. Пусть 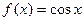 . Эта функция также бесконечно дифференцируема
. Эта функция также бесконечно дифференцируема 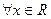 . Поскольку здесь
. Поскольку здесь
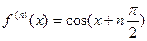 ,
,
то
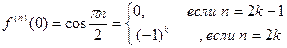
Поэтому имеем,
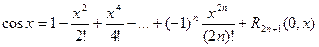
при этом остаточный член имеет вид:
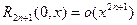
(в форме Пеано);
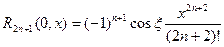
(в форме Лагранжа);
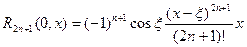
(в форме Коши).
Приведем без доказательства еще несколько разложений по формуле Маклорена:
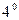 .
. 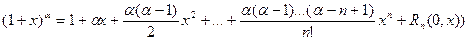
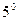 .
. 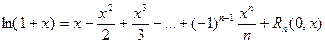
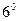 .
. 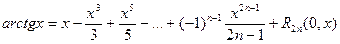
 2014-02-09
2014-02-09 1588
1588
