nо 1. Таблица производных
Элементарные функции (за исключением функций 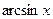 и
и 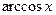 ) дифференцируемы в своих областях определения, причем справедливы следующие формулы (они обосновываются в следующих пунктах):
) дифференцируемы в своих областях определения, причем справедливы следующие формулы (они обосновываются в следующих пунктах):
 .
. 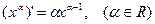
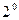 .
. 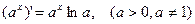
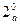 .
. 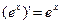
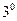 .
. 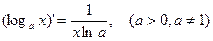
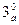 .
. 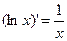
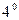 .
. 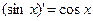
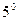 .
. 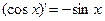
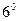 .
. 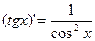
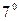 .
. 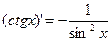
 .
. 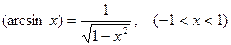
 .
. 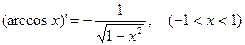
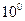 .
. 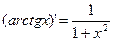
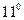 .
. 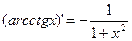
Определим так называемые гиперболические функции:
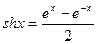 - гиперболический синус;
- гиперболический синус;
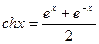 - гиперболический косинус;
- гиперболический косинус;
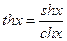 - гиперболический тангенс;
- гиперболический тангенс;
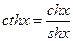 - гиперболический котангенс.
- гиперболический котангенс.
Для гиперболических функций справедливы следующие формулы:
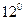 .
. 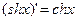
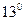 .
. 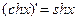
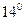 .
. 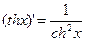
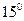 .
. 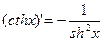
nо 2. Показательная и логарифмическая функции.
Здесь будут установлены формулы 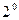 ,
, 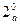 ,
, 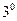 и
и 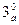 из предыдущего пункта. Прежде всего, вычислим некоторые пределы.
из предыдущего пункта. Прежде всего, вычислим некоторые пределы.
Покажем, что
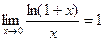 | (1) |
Как было установлено ранее
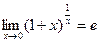 .
.
Поэтому, доопределив функцию f(x) = 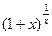 в точке
в точке 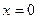 равенством
равенством 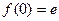 можно считать, что она непрерывна в этой точке. Учитывая это, а также то, что функция
можно считать, что она непрерывна в этой точке. Учитывая это, а также то, что функция 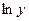 непрерывна в точке
непрерывна в точке 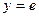 , по теореме о непрерывности суперпозиции непрерывных функций будем иметь
, по теореме о непрерывности суперпозиции непрерывных функций будем иметь
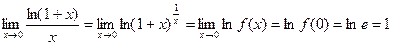 .
.
Следовательно, равенство (1) действительно имеет место.
Покажем теперь, что
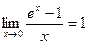 | (2) |
Доопределим функцию 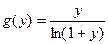 в точке
в точке 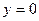 равенством
равенством 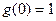 . В силу равенства (1) можно считать, что она непрерывна в этой точке. Положим
. В силу равенства (1) можно считать, что она непрерывна в этой точке. Положим 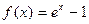 . Эта функция непрерывна на всей вещественной оси и, в частности, непрерывна в точке
. Эта функция непрерывна на всей вещественной оси и, в частности, непрерывна в точке 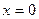 , при этом
, при этом  . Тогда по теореме о непрерывности суперпозиции непрерывных функций сложная функция
. Тогда по теореме о непрерывности суперпозиции непрерывных функций сложная функция 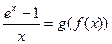 непрерывна в точке
непрерывна в точке 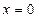 . Поэтому будем иметь
. Поэтому будем иметь
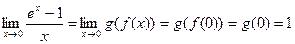 .
.
Таким образом равенство (2) доказано.
Теперь используя равенство (2) и то, что постоянную можно выносить за знак предела получим:
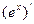 =
=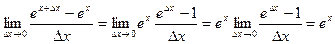
Таким образом установлена формула 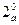 .
.
Далее, так как функция 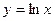 является обратной к функции
является обратной к функции 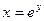 , по формуле для производной обратной функции имеем:
, по формуле для производной обратной функции имеем:
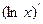 =
=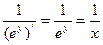 .
.
Следовательно, установлена и формула 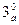 .
.
Для вывода формулы 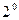 установим формулу дифференцирования показательно-степенной функции.
установим формулу дифференцирования показательно-степенной функции.
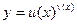
где 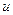 и
и 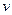 – дифференцируемые на некотором промежутке
– дифференцируемые на некотором промежутке 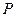 функции, причем
функции, причем 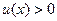 на
на 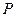 .
.
Используя формулу для производной сложной функции, формулы 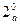 и
и 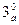 , а также формулу для производной произведения функций будем иметь
, а также формулу для производной произведения функций будем иметь
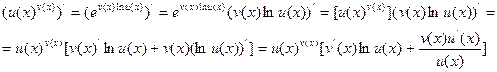
Таким образом,
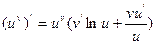 .
.
В частности, если здесь 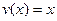 , а
, а 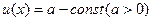 , то
, то
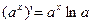 ,
,
т.е. установлена и формула 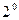 . Формула
. Формула 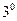 вытекает из нее в силу формулы дифференцирования обратной функции:
вытекает из нее в силу формулы дифференцирования обратной функции:
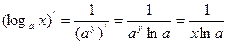
(здесь 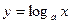 ,
, 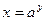 ).
).
nо 3. Производная степенной функции.
Производную от степенной функции 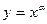 (
(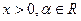 ) можно вычислить с помощью формулы дифференцирования сложной функции, предварительно представив функцию
) можно вычислить с помощью формулы дифференцирования сложной функции, предварительно представив функцию 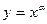 в виде
в виде 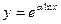 :
:
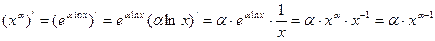
Формула 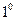 , таким образом, также доказана.
, таким образом, также доказана.
nо 4. Тригонометрические функции.
Используя формулу
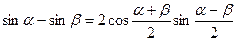 ,
,
а также известный замечательный предел
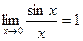 ,
,
по определению производной с учетом непрерывности функции 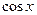 будем иметь
будем иметь
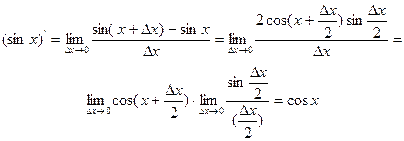
Далее, по правилу дифференцирования сложной функции получим
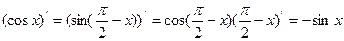
Производные от функции 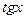 и
и 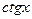 вычисляются с использованием установленных выше формул
вычисляются с использованием установленных выше формул 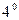 и
и 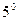 и формул дифференцирования частного. Читателю предлагается сделать это самостоятельно.
и формул дифференцирования частного. Читателю предлагается сделать это самостоятельно.
nо 5. Обратные тригонометрические функции.
Формулы 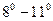 выводятся с помощью формулы для производной обратной функции и одной из соответствующих
выводятся с помощью формулы для производной обратной функции и одной из соответствующих 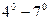 .
.
Например, функция
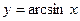
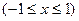
Является обратной к функции 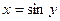 , (
, (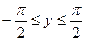 ). Поэтому
). Поэтому
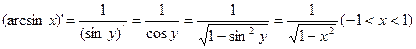
Перед радикалом здесь берется знак «+», поскольку 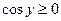 при
при 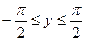 .
.
Аналогично вычисляется производная от функции 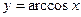
Далее, функция 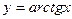
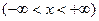 является обратной к функции
является обратной к функции 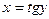
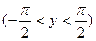 . Поэтому
. Поэтому
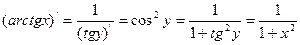
Аналогично вычисляется производная от функции 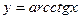
 2014-02-09
2014-02-09 2868
2868
