2014-02-09
2395
Определение 1. Пусть функция 
определена на множестве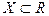 
и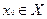 
.Говорят, что в точке 
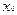функция имеет локальный минимум (локальный максимум) , если существует такая окрестность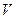 
этой точки, что
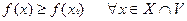 | (1) |
( ), |
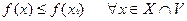при этом точку 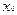называют точкой локального минимума (локального максимума) функции.
Замечание 1. Если 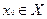внутренняя точка множества 
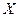, т.е. если она принадлежит ему вместе с некоторой своей окрестностью то в условии (1) вместо «
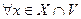» можно писать «
».
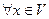Замечание 2. Если в точке 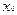функция имеет или локальный минимум или локальный максимум, то говорят, что в ней она имеет локальный экстремум,при этом её саму называют точкой локального экстремума.
Замечание 3. Всякая точка максимума (минимума) фуркции на множестве 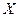, т.е. всякая точка 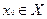, для которой
 |
( ), |
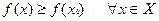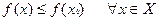иногда называется точкой глобального минимума (глобального максимума) функции на множестве .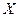
Очевидно, что всякая точка глобального экстремума, т.е. глобального максимума или глобального минимума, является также и точкой локального экстремума.
Теорема 1(Ферма). Пусть функция определена на множестве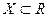 
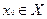, , при этом 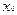- внутренняя точка множества 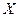и функция дифференцируема в этой точке.Тогда, если 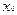– точка локального экстремума этой функции, то
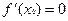 . | (2) |
Д о к а з а т е л ь с т в о. Для определенности будем считать, что 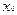─ точка локального минимума.Тогда 
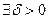такое, что 
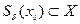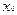( ─ внутренняя точка 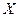) и
.
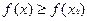
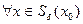Поэтому
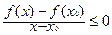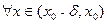   | (3) |
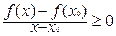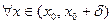  . | (4) |
Из неравенства (3), в силу дифференцируемости функции в точке 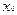и теоремы о предельном переходе в неравенстве, очевидно следует, что
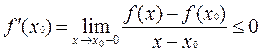 | (5) |
а из неравенства (4), в силу того же, в свою очередь, следует, что
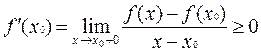 | (6) |
из неравенств (5) и (6) и вытекает равенство (2) □
