Первого порядка

Интегрируемые виды дифференциальных уравнений

Тип 1. Уравнение с разделяющимися переменными.

Уравнения вида M₁(x)N₁(y)dx+M₂(x)N₂(y)dy=0 (1) или 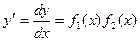(2), а также уравнения, которые с помощью алгебраических преобразований приводятся к уравнениям, называются уравнениями с разделяющимися переменными.

Уравнение вида 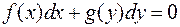называется дифференциальным уравнением с разделенными переменными.

Его общим интегралом будет 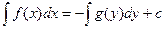, где с – произвольная постоянная.

Алгоритм решения:

1. Преобразовать уравнение с разделяющимися переменными к уравнению с разделенными переменными.

2. Проинтегрировать обе части уравнения.

Примеры. 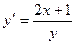, 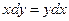- уравнения с разделяющимися переменными.