Дифференциальные уравнения первого порядка. Основные понятия

Тема 2. Дифференциальные уравнения.

Дифференциальным называют уравнение, из которого требуется определить искомую функцию и которое содержит не только эту функцию, но и ее производные или дифференциалы.

Если неизвестная функция является функцией одной переменной, то такое уравнение называют обыкновенным дифференциальным уравнением.

Пример 1.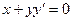

Если неизвестная функция является функцией нескольких переменных, то такое уравнение называют уравнением в частных производных.

Пример.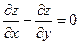

Порядком дифференциального уравнения называют наивысший порядок содержащихся в нем производных.

Пример 2. 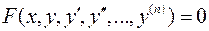дифференциальное уравнение 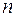-го порядка.

Решением дифференциального уравнения называют функцию 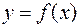, дифференцируемую по крайней мере 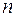раз, обращающую его при подстановке в уравнение в тождество.

Отыскание всех решений и описание их свойств является основными задачами теории дифференциальных уравнений. Процесс отыскания решений называют интегрированием этого уравнения.

Пример 3.

Найти все решения дифференциального уравнения .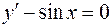

Интегрируя, получим .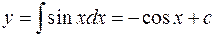

Общим решением дифференциального уравнения называют решение, которое существенно зависит от произвольной постоянной с. Общее решение, полученное в неявном виде называется общим интегралом дифференциального уравнения.

y = - cos x +c – общее решение.

y + cos x = с – общий интеграл.

Решение дифференциального уравнения, которое получается из общего решения при фиксированном значении постоянной c, называют частным решением.

Пусть М(0,2), с= 2+ сos(0); с = 3. y = -cos x + 3 – частное решение, то есть мы выделяем кривую, которая проходит через точку (0,2).

Кривые y = - cos x +c называются интегральными кривыми дифференциального уравнения .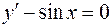

Уравнение вида F(x,y,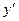)=0 (1) называется дифференциальным уравнением первого порядка.

Задача Коши для дифференциального уравнения первого порядка заключается в отыскании решения уравнения (1), удовлетворяющего начальному условию 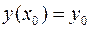. Геометрически это означает определение интегральной кривой, проходящей через точку .

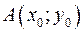Теорема Пикара. Если в уравнении 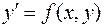функция 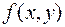определена и непрерывна в окрестности точки 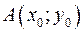и, кроме того, имеет частную производную 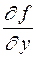, то задача Коши имеет единственное решение, являющееся дифференцируемой функцией. Если в точке 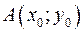условия теоремы Пикара нарушаются, то задача Коши может иметь несколько решений или не иметь их вовсе. В первом случае через точку 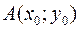проходит несколько интегральных кривых. Точки, в которых происходит нарушение условий теоремы Пикара, называют особыми. Дополнительные решения задачи Коши, возникающие при этом, также называют особыми.