Приёмы корреляционного анализа

Приёмы корреляционного анализа используются для измерения влияния факторов в стохастическом анализе, когда взаимосвязь между показателями неполная, вероятностная. Различают парную и множественную корреляцию. Парная корреляция – это связь между двумя показателями, один из которых является факторным, а другой результативным. Множественная корреляция – возникает от взаимодействия нескольких факторов с результативным показателем.

Необходимые условия применения корреляционного анализа.

1. Наличие достаточно большого количества наблюдений о величине исследуемых факторных и результативных показателей.

2. Исследуемые факторы должны иметь количественное измерение и отражение в тех или иных источниках информации.

Применение корреляционного анализа позволяет решить следующие задачи:

1. определить изменение результативного показателя под воздействием одного или нескольких факторов, т.е. определить, на сколько единиц изменяется величина результативного показателя при изменении факторного на единицу;

2. Установить относительную степень зависимости результативного показателя от каждого фактора.

Корреляционный анализ состоит из нескольких этапов.

На первом этапе определяются факторы, которые оказывают воздействие на изучаемый показатель, и отбираются наиболее существенные для корреляционного анализа. Отбор факторов – очень важный момент в экономическом анализе: от того, насколько правильно он сделан, зависит точность выводов по итогам анализа. При этом необходимо придерживаться следующих правил:

1) при отборе факторов в первую очередь следует учитывать причинно- следственные связи между показателями, ибо только они раскрывают сущность изучаемых явлений. Анализ же таких факторов, которые находятся в математических соотношениях с результативным показателем, не имеет практического смысла;

2) при создании многофакторной корреляционной модели необходимо отбирать самые значимые факторы, которые оказывают наиболее существенное воздействие на результативный показатель, так как охватить все условия и обстоятельства фактически невозможно. Факторы, которые имеют критерий надежности по Стьюденту меньше табличного, не рекомендуется принимать в расчет;

3) в корреляционную модель линейного типа не рекомендуется включать факторы, связь которых с результативным показателем носит криволинейный характер;

4) не рекомендуется включать в корреляционную модель взаимосвязанные факторы. Если парный коэффициент корреляции между двумя факторами больше 0,85, то по правилам корреляционного анализа один из них необходимо исключить, иначе это приведет к искажению результатов анализа;

5) нельзя включать в корреляционную модель факторы, связь которых с результативным показателем носит функциональных характер.

Большую помощь при отборе факторов для корреляционной модели оказывают аналитические группировки, способ сравнения параллельных и динамических рядов, линейные графики. С их помощью можно определить наличие, направление и форму зависимости между изучаемыми показателями. Отбор факторов можно производить также в процессе решения задачи корреляционного анализа на основе оценки их значимости по критерию Стьюдента, о котором будет сказано ниже.

На втором этапе собирается исходная информация по каждому факторному и результативному показателю. Она должна быть проверена на достоверность, на однородность и на соответствие закону нормального распределения.

В первую очередь необходимо убедиться в достоверности информации, насколько она соответствует объективной действительности. Использование недостоверной, неточной приведет к неточным результатам анализа и к неправильным выводам.

Одно из условий корреляционного анализа – однородность используемой информации Относительно распределения ее около среднего уровня. Если в совокупности имеются группы объектов, которые значительно отличаются от среднего уровня, то это говорит о неоднородности исходной информации.

Критерием однородности информации служат среднеквадратическое отклонение и коэффициент вариации, которые рассчитываются по каждому факторному и результативному показателю.

Среднеквадратическое отклонение показывает абсолютное отклонение индивидуальных значений от среднеарифметической. Оно определяется по формуле:

.

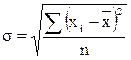Коэффициент вариации показывает относительную меру отклонений отдельных значений от среднеарифметической. Для его расчета используется формула:

.

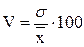Чем выше коэффициент вариации, тем относительно больший разброс и меньшая выравненность изучаемых объектов. Изменчивость вариационного ряда принято считать незначительной, если вариация не превышает 10%, средней – если вариация составляет 10 – 12%, значительной – когда она больше 20%, но не превышает 33%. Если же вариация выше 33%, то это свидетельствует о неоднородности информации и о необходимости исключения нетипичных наблюдений, которые обычно бывают в первых и последних ранжированных рядах выборки.

Следующее требование к исходной информации – подчинение ее закону нормального распределения. Для количественно оценки степени отклонения информации от нормального распределения служат отношения показателя асимметрии к ее ошибке и отношение показателя эксцесса к его ошибке.

Показатель асимметрии (А) и его ошибка (m_а) рассчитываются по следующим формулам:

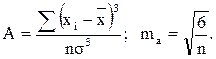
Показатель эксцесса (Е) и его ошибка (m_е) рассчитываются следующим образом:

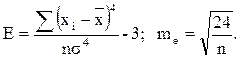
В симметричном распределении А=0. Отклонение от нуля указывает на наличие ассиметрии в распределении данных около средней величины. Отрицательная ассиметрия свидетельствует о том, что преобладают данные с большими значениями, а с меньшими значениями встречаются значительно реже. Положительная ассиметрия показывает, что чаще встречаются данные с небольшими значениями.

В нормальном распределении показатель эксцесса Е=0. Если Е >0, то данные густо сгруппированы около средней, образуя островершинность. Если Е<0, то кривая распределения будет плосковершинной. Однако когда отношения А/m_a и Е/m_e меньше 3, то ассиметрия и эксцесс не имеют существенного значения и исследуемая информация соответствует закону нормального распределения. Следовательно, её можно использовать для корреляционного анализа.

На третьем этапе изучается характер и моделируется связь между факторными и результативными показателями, т.е. подбирается и обосновывается математическое уравнение, которое наиболее точно выражает сущность исследуемой зависимости. Для его обоснования используются те же приёмы, что и для установления наличия связи: аналитические группировки, линейные графики и др.