Критерий устойчивости Гурвица. Критерии устойчивости

Критерии устойчивости

Алгебраические критерии устойчивости представляют собой совокупность требований, которым должны удовлетворять коэффициенты характеристического уравнения для того, чтобы все корни его находились в левой полуплоскости. К таким критериям относятся критерии устойчивости Вышнеградского, Рауса, Гурвица, Михайлова и ряд других.

Согласно критерию устойчивости Гурвица, для устойчивости системы необходимо и достаточно, чтобы все коэффициенты характеристического уравнения

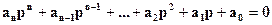
имели один и тот же знак, а определитель порядка (n-1) и все его диагональные миноры были бы положительными:

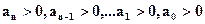
и

.

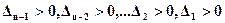Правило составления определителей:

D₁=а_п-1>0;

D₂= а_п-1 а_п-3 =а_п-1× а_п-2 – а_п× а_п-3 >0;

а_п а_п-2

а_п-1 а_п-3 а_п-5

D₃= а_п а_п-2 а_п-4 =а_п-3×D₂ – а_п-1 а_п-1 а_п-5 =а_п-3×D₂ – а_п-1(а_п-1 × а_п-4 - а_п× а_п-5)>0;

0 а_п-1 а_п-3 а_п а_п-4

а_п-1 а_п-3 а_п-5 а_п-7

D₄= а_п а_п-2 а_п-4 а_п-6 =а_п-4× D₃>0

0 а_п-1 а_п-3 а_п-5

0 а_п а_п-2 а_п-4

и т.д.

Все коэффициенты, имеющие индекс, превышающий степень характеристического уравнения, заменяются нулями.

Определитель D_п-1 называется определителем Гурвица, а D₁, D₂,… D_п-2 представляют собой диагональные миноры определителя Гурвица.

Итак, корни характеристического уравнения имеют отрицательную вещественную часть, если все определители положительны.

Отсюда следует, что система заведомо неустойчива, если какой-либо из ее коэффициентов характеристического уравнения отличается по знаку от остальных коэффициентов или равен нулю.

Примеры устойчивости простейших линейных систем:

1. Система а₁р+а₀=0

условие устойчивости: а₁>0; а₀ >0.

2. Система а₂р²+а₁р+а₀=0

условие устойчивости: а₂>0; а₁>0; а₀>0.

3. Система а₃р³+а₂р²+а₁р+а₀=0

условие устойчивости: а₃>0; а₂>0; а₁>0; а₀>0; а₂×а₁>а₃×а₀.