Понятие устойчивости систем автоматического управления

Линейная система автоматического управления является устойчивой, если после снятия возмущающего воздействия она возвращается к состоянию равновесия (рис. 1 – 55а). Если в системе автоматического управления после снятия возмущающего воздействия возникают незатухающие колебания, то система находится на границе устойчивости (рис. 1 – 55б). Если же в системе автоматического управления возникают расходящиеся колебания, то система будет не устойчивой (1 – 55в).

Указанное нестрогое определение устойчивости систем автоматического управления будет правомочно лишь для линейных систем, в то время как для определения устойчивости нелинейных систем вводится понятие устойчивости систем в «малом» и «большом», если независимо от величины возмущающего воздействия она возвращается в равновесное состояние.

Физической интерпретацией такой системы может служить вогнутая поверхность (рис. 1 – 56а), на дне которой находится шарик: независимо от того, в каком положении находится этот шарик, он по истечении какого-то времени вернется в нижнее положение. Система автоматического управления будет устойчива в «малом», если она возвращается в равновесное состояние только при небольших возмущающих воздействиях, а при больших возмущениях она становится неустойчивой или переходит в новое состояние равновесия.

Физической интерпретацией такой системы может служить поверхность на рис. 1 – 56б, наглядно показывающая, что при небольших первоначальных отклонениях шарика от исходного состояния он возвращается в состояние равновесия, а при значительных первоначальных отклонениях шарик не возвращается в исходное состояние равновесия, т.е. система будет неустойчивой. Такими свойствами обладают нелинейные системы автоматического управления, которые в зависимости от величины возмущающего воздействия могут быть либо устойчивыми, либо неустойчивыми. Следовательно, устойчивость системы автоматического управления в «малом» является характерной особенностью нелинейной системы.

Линейные системы, устойчивые в «малом», будут устойчивы и в «большом».

Для выявления причин устойчивости или неустойчивости систем автоматического управления рассмотрим линейное дифференциальное уравнение, описывающее динамические свойства системы

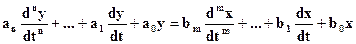. (1-84)

Свободное движение этой системы (см. § 1-5) определяется видом левой части, которая в определенной форме записывается следующим образом:

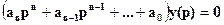. (1-85)

Тогда решение дифференциального уравнения (84) следует искать в виде:

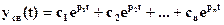. (1-86)

Отсюда следует, что для того, чтобы система была устойчивой, необходимо, чтобы все слагаемые уравнения (86) с течением времени стремились к нулю. Последнее будет наблюдаться только в том случае, когда все корни – Р_i характеристического уравнения:

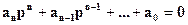(1-87)

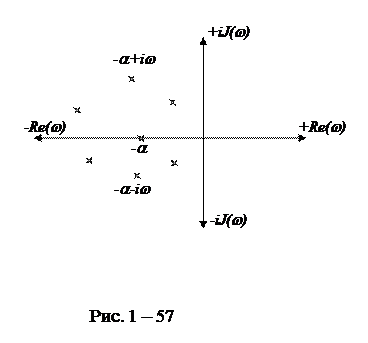
будут вещественными отрицательными – P_i=-a или комплексные с отрицательной действительной частью – P_i=-a±iw.

Таким образом необходимым условием устойчивости линейной системы является расположение корней характеристического уравнения в комплексной плоскости левее мнимой оси (рис. 1 – 57).

К сожалению, вычисление корней характеристического уравнения часто является очень сложной и громоздкой задачей. Однако для оценки устойчивости системы управления не обязательно точное знание корней характеристического уравнения, а достаточно лишь знать их расположение в комплексной плоскости, т.е знак вещественной части корней характеристического уравнения.

Эта особенность существенно облегчает анализ систем управления и приводит к тому, что устойчивость систем автоматического управления исследуют с помощью оценок, называемых критериями устойчивости, тесно связанных с коэффициентами характеристического уравнения.

При анализе и синтезе АСУ широко исследуются следующие критерии устойчивости:

1) алгебраические критерии устойчивости;

2) критерий устойчивости Михайлова;

3) амплитудно-фазовый критерий устойчивости.