Произведено 11 измерений сопротивления резистора в ряду. Получены следующие результаты:
1. 9791
2. 9795
3. 9789
4. 9794
5. 9796
6. 9800
7. 9793
8. 9795
9. 9765
10. 9794
11. 9797 Ом
1. Находим среднее арифметическое
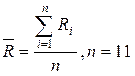
Rср = 9794,4 Ом
2. Находим остаточные суммы
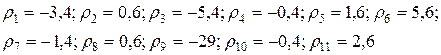
Сразу обращает на себя внимание результат ρ9. Это очень большая остаточная сумма по своей величине, по-видимому, это – промах. Выделим 9-й результат.
3. Находим сумму всех ρ. Она оказывается из-за девятого результата весьма большой и далекой от 0. Проверим общую сумму, отбросив девятый результат. В этом случае сумма ρ оказывается равна 0. Это еще раз подтверждает, что девятый результат измерений следует исключить даже без проверки на критерий 3σ.
Итак, в ряду осталось 10 результатов. Для них следует посчитать Rср. Приведенное ранее Rср как раз и соответствует числу измерений, равному 10, следовательно, повторять измерения по отысканию Rср не будем.
4. Возводим все ρi в квадрат.
5. Находим 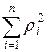
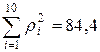 .
.
6. Находим оценку СКО:
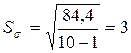
Проверим для верности наличие промахов в прежнем ряду. По подсчетам 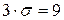 , что гораздо меньше, чем 29, что соответствует ρ9.
, что гораздо меньше, чем 29, что соответствует ρ9.
7. Находим СКО среднего арифметического:
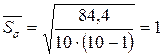
Задаемся вероятностью, что полученный результат окажется в интервале, определяемом вычисленной погрешностью 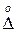 .
. 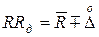
Вероятность р = 0,95.
Коэффициент Стьюдента для n = 10 и p = 0,95 равен 2,3. Тогда действительное значение 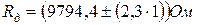 .
.
Тогда окончательный результат должен быть в виде:
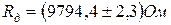 р=0,95.
р=0,95.
Возможна и другая запись:
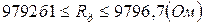 с вероятностью р = 0,95.
с вероятностью р = 0,95.
Второй вариант этой же задачи, если не считать девятый результат промахом:
| R | 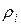 | 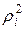 |
| -0,727 | 0,5285 | |
| 3,273 | 10,713 | |
| -2,727 | 7,437 | |
| 2,273 | 5,167 | |
| 4,273 | 18,259 | |
| 8,273 | 68,44 | |
| 1,273 | 1,62 | |
| 3,273 | 10,71 | |
| -26,727 | 714,33 | |
| 2,273 | 5,167 | |
| 5,273 | 27,81 | |
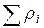 =0,003 =0,003 | 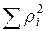 =870,1815 =870,1815 | |
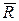 =9791,7 =9791,7 |
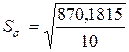 = 9,328;
= 9,328;
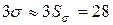 ;
; 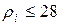
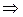 промаха нет.
промаха нет.
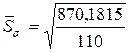 =2,813;
=2,813;
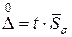 =2,23×2,813 = 6,272;
=2,23×2,813 = 6,272;
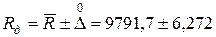 ;
;
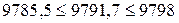 .
.
 2014-02-18
2014-02-18 1551
1551








