Вычисление случайных погрешностей измерений.
Величину отдельной случайной погрешности, в отличие от систематической, вычислить невозможно, хотя эти погрешности реально существуют и искажают результат измерения. Чтобы учесть эти погрешности, приходится делать многократные измерения одной и той же величины (получать ряд измерений). Этот ряд измерений имеет разброс в значениях для каждого конкретного измерения. Интуитивно, за наиболее вероятную величину полученных результатов следует принять их среднее арифметическое. Вероятность того, что это среднее арифметическое будет истинным значением, равна единице, если мы проведем бесконечно большое число измерений. Реально это невозможно. В лучшем случае проводят более 30 измерений, а обычно около 10. В этом случае законы математической статистики и теории вероятностей, которые следовало бы использовать при вычислениях истинного результата, дают сбой. Приходится делать допущения, что уменьшает точность измерений. Любые случайные величины, а случайные погрешности являются таковыми, распределяются особым образом, то есть имеют свои законы распределения. Этих законов достаточно много и при каждом из них нужно производить свой алгоритм вычислений. Так как число измерений обычно не превышает 15, то показано, что эти случайные погрешности можно довольно точно описать, пользуясь нормальным (гауссовым) распределением.
1. Находим среднее арифметическое результатов ряда измерений 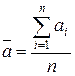 .
.
2. Находим остаточные суммы, каждая из которых равна разности между результатом отдельного измерения и средним значением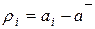 .
.
3. Сумма этих остаточных сумм ρi должна быть минимальной, то есть весьма близкой к нулю (с учетом знаков) 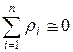 . Если это не так, то в ряду измерений имеется промах, то есть результат, который получен ошибочно. Его численное значение заметно отличается от значений других результатов. Делается анализ ряда измерений, и отмечаются подозрительные результаты.
. Если это не так, то в ряду измерений имеется промах, то есть результат, который получен ошибочно. Его численное значение заметно отличается от значений других результатов. Делается анализ ряда измерений, и отмечаются подозрительные результаты.
4. Все остаточные суммы возводятся в квадрат ρi2.
5. Находится сумма квадратов остаточных сумм 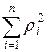 .
.
6. Находим среднеквадратичное отклонение (СКО) ряда измерений 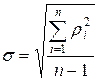 . Эта формула для σ выполняется точно лишь при
. Эта формула для σ выполняется точно лишь при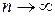 . Так как такого числа измерений обычно не производят, то полученный по такой формуле результат называют оценкой СКО
. Так как такого числа измерений обычно не производят, то полученный по такой формуле результат называют оценкой СКО 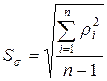 ,
, 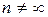 .
.
7. Зная оценку СКО Sσ, можно вычислить величину, примерно равную интервалу 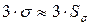 . Показано, что ни одно из ρi не должно превышать интервала 3σ
. Показано, что ни одно из ρi не должно превышать интервала 3σ 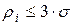 . Если имеется результат, для которого это условие не выполняется, то этот результат – промах. Его нужно исключить и считать, что в ряду будет результатов на один меньше. Далее придется повторить все предыдущие вычисления, так как ряд имеет меньшее число результатов и, если после новой проверки по п. 7 условие будет выполнимо для всех результатов, то можно продолжать обработку результатов.
. Если имеется результат, для которого это условие не выполняется, то этот результат – промах. Его нужно исключить и считать, что в ряду будет результатов на один меньше. Далее придется повторить все предыдущие вычисления, так как ряд имеет меньшее число результатов и, если после новой проверки по п. 7 условие будет выполнимо для всех результатов, то можно продолжать обработку результатов.
8. Вычисляется оценка СКО 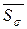 среднего арифметического ряда результатов. Эту оценку
среднего арифметического ряда результатов. Эту оценку 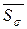 можно назвать также СКО результата измерений
можно назвать также СКО результата измерений 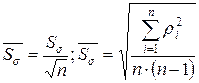 .
.
9. Так как в ряду измерений имеется  , то корректно ввести поправочный коэффициент, который бы позволил получить значение погрешности результата измерений более точно, чем погрешность, численно равная
, то корректно ввести поправочный коэффициент, который бы позволил получить значение погрешности результата измерений более точно, чем погрешность, численно равная  . Такому случаю при нормальном распределении результатов соответствует распределение Стьюдента (Стьюдент – псевдоним английского ученого Госсета, который будучи еще студентом применил это распределение). Используя коэффициент Стьюдента, можно определить погрешность результата для каждого конкретного ряда измерений, то есть найти наиболее вероятную погрешность окончательного результата ряда измерений
. Такому случаю при нормальном распределении результатов соответствует распределение Стьюдента (Стьюдент – псевдоним английского ученого Госсета, который будучи еще студентом применил это распределение). Используя коэффициент Стьюдента, можно определить погрешность результата для каждого конкретного ряда измерений, то есть найти наиболее вероятную погрешность окончательного результата ряда измерений  , которая равна
, которая равна 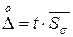 ,
, 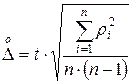 ; t – коэффициент Стьюдента. Его значение дается в таблицах. Его значение находят по заданной вероятности результатов измерений и по числу измерений в ряду.
; t – коэффициент Стьюдента. Его значение дается в таблицах. Его значение находят по заданной вероятности результатов измерений и по числу измерений в ряду.
10. Записываем результат измерения, который будет верным с выбранной нами вероятностью. Этот результат будет: 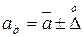 с вероятностью p.
с вероятностью p.
 2014-02-18
2014-02-18 1225
1225
