2014-02-18
1145
Влияние начального состояния на вероятность нахождения системы в том или ином состоянии исчезает с ростом времени, т.е. вероятности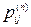 
сходятся к предельным значениям 
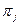, не зависящим от i и образующим распределение вероятностей: 
.
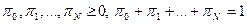Следующая теорема описывает широкий класс цепей Маркова, обладающих так называемым свойством эргодичности: пределы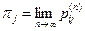 
не только существуют, не зависят от i, образуют распределение вероятностей, но и таковы, что 
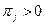для всех j.
Теорема (Эргодическая). Пусть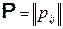 
матрица переходных вероятностей цепи Маркова с конечным множеством состояний 
.
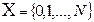А) Если найдется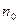 
такое, что
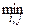
то существуют числа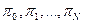 
такие, что
,
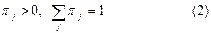и для любого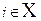 
.
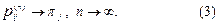Б) Обратно, если существуют числа 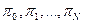, удовлетворяющие условиям (2), (3), то найдется 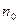такое, что выполнено условие (1).
С) Числа 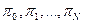удовлетворяют системе уравнений
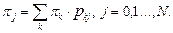
Отметим, что последняя система играет большую роль в теории цепей Маркова. Всякое её неотрицательное решение (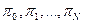), удовлетворяющее условию 
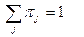принято называть стационарным или инвариантным распределением вероятностей для цепей Маркова.
В заключение этого раздела перечислим основные вопросы, связанные с цепями Маркова.
1) Существуют ли пределы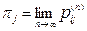 
, не зависящие от i?
2) Образуют ли пределы (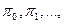
) распределение вероятностей, т.е. 
?
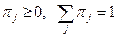3) Является ли цепь эргодической, т.е. таковы ли пределы (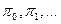
), что 
?
4) Существует ли единственное стационарное распределение вероятностей (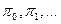), т.е такие, что 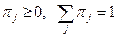и 
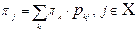, где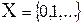 
Для получения ответа на эти вопросы сначала проведем классификацию состояний цепи Маркова.
