Рассмотрим последовательность случайных величин x 1, x 2, …, xn, и предположим, что k и l индексы такие, что 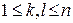 и
и 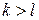 .
.
Определение. Последовательность случайных величин x 1, x 2, …, xn образуют мартингал, если имеет место равенство (равенство мартингала):
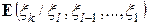 = xl,
= xl,
и образуют субмартингал, если имеет место неравенство:
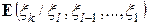
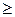 xl.
xl.
Пример. Пусть h 1, h 2, …, hn независимые случайные величины с E hj = 0 для всех j = 1,2 ,…,n. Определим xk = 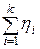 . Покажем, что последовательность x 1, x 2, …, xn образуют мартингал. Пусть
. Покажем, что последовательность x 1, x 2, …, xn образуют мартингал. Пусть 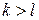 , тогда xk =
, тогда xk = 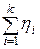 = xl +
= xl + 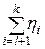 , поэтому
, поэтому 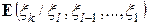 =
= 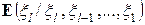 +
+ 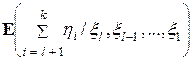 . Так как случайная величина xl измерима относительно
. Так как случайная величина xl измерима относительно 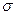 - алгебры A(x1, x2, …, xl), отсюда следует, что
- алгебры A(x1, x2, …, xl), отсюда следует, что 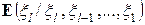 = xl. По условию, h 1, h 2, …, hn независимые случайные величины, поэтому
= xl. По условию, h 1, h 2, …, hn независимые случайные величины, поэтому 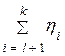 не зависит от
не зависит от 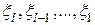 , следовательно, по свойству 7 условного математического ожидания (см. 2.9.1)
, следовательно, по свойству 7 условного математического ожидания (см. 2.9.1)
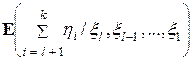 =
= 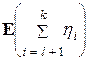 =
= 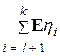 = 0.
= 0.
Таким образом, мы получили 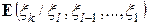 = xl, т.е. последовательность x 1, x 2, …, xn образуют мартингал.
= xl, т.е. последовательность x 1, x 2, …, xn образуют мартингал.
В заключение без доказательства приведем несколько полезных утверждений.
Теорема 1. Пусть последовательность случайных величин x 1, x 2, …, xn образуют мартингал и предположим, что 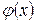 выпуклая функция. Тогда последовательность случайных величин
выпуклая функция. Тогда последовательность случайных величин 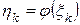 , k = 1,2,…, n образуют субмартингал.
, k = 1,2,…, n образуют субмартингал.
Теорема 2. Пусть последовательность случайных величин x 1, x 2, …, xn образуют субмартингал и предположим, что k и l индексы такие, что 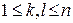 и
и 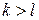 . Пусть A(x 1, x 2, …, xl) = A -
. Пусть A(x 1, x 2, …, xl) = A - 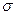 -алгебра, порожденная случайными величинами x 1, x 2, …, xl. Тогда выполняется неравенство:
-алгебра, порожденная случайными величинами x 1, x 2, …, xl. Тогда выполняется неравенство:
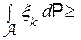
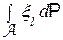 .
.
Теорема 3. Пусть последовательность случайных величин x 1, x 2, …, xn образуют субмартингал, тогда имеет место
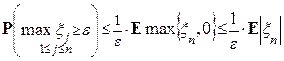
 2014-02-18
2014-02-18 2019
2019








