Задачи к 2.8

Классификация состояний цепи Маркова

Определение 1. Будем называть состояние 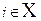несущественным, если из него с положительной вероятностью можно за конечное число шагов выйти, но нельзя в него вернуться, т.е. существуют такие m и j, что 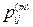> 0, но для всех n и j .

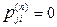Состояния, которые не являются несущественными называются существенными. Рассмотрим множество существенных состояний.

Определение 2. Существенные состояния i и j называются сообщающимися, если существуют такие n и m, что 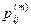> 0 и .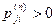

Следовательно, множество существенных состояний разбиваются на конечное или счетное число непересекающихся множества 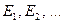, такие, что переходы между различными множествами невозможны. Эти множества называются неразложимыми. Если цепь состоит из одного неразложимого класса, то такая цепь называется неразложимой или неприводимой цепью.

Определение 3. Состояние j имеет период d=d(j), если выполнены следующие условия:

1) 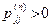только для тех n, которые имеют вид n = dm (m – целое число);

2) d есть наименьшее из чисел, удовлетворяющих условию 1).

Замечание. Если 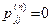для всех n > 1, то полагаем, что d (j)=0. Если же d (j)=1, то состояние j называется апериодическим.

Если цепь Маркова неразложимая, т.е состоит из одного класса сообщающихся существенных состояний, то, если одно состояние имеет период d, все состояния также имеют тот же период, и он называется периодом этого класса (или периодом цепи Маркова).

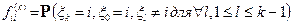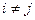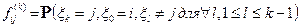Обозначим через - вероятность первого возвращения в состояние i за k шагов; и для через - вероятность впервые попасть в состояние j за k шагов, выйдя из состояния i.

Теперь без доказательства приведем следующую формулу:

.

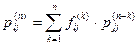Обозначим через 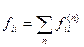- вероятность рано или поздно вернуться впервые в состояние i, выйдя из него.

Определение 4. Состояние i называется возвратным, если 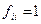, и невозвратным, если .

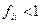Далее, обозначим через .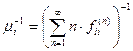

Определение 5. Возвратное состояние i называется положительным, если 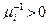, и нулевым, если .

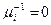В заключение этого раздела сформулируем несколько полезных теорем без доказательств.

Теорема 1. А) Состояние i возвратное тогда и только тогда, когда

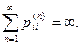
В) Если состояние j возвратное, и i и j – сообщающиеся состояния, то состояние i тоже возвратное.

Теорема 2. В неразложимой цепи Маркова все состояния принадлежат одному типу, а именно

1) Если хотя бы одно состояние возвратное, то все остальные - тоже.

2) Если хотя бы одно состояние нулевое, то все остальные - тоже.

3) Если хотя бы одно состояние периодическое, то все остальные – тоже с одним и тем же периодом.

Теорема 3. Пусть цепь Маркова неразложимая, непериодическая. Тогда существуют пределы 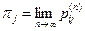, и при этом

А) все они равны нулю, если все состояния невозвратные или возвратные нулевые;

В) все они положительные, если все состояния возвратные ненулевые, и они находятся как решение следующей системы уравнений

.

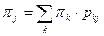1. Книги А, В и С лежат в стопке. С вероятностью 1/3 выбирается одна из книг и кладется сверху. Состояние цепи Маркова – порядок книг в стопке. Провести полный анализ этой цепи Маркова.

2.В двух урнах размещены три шара. С вероятностью 1/3 достают один из трех шаров и перекладывают его на урну, в которой он находится, в другую. Состояние цепи Маркова – число шаров в первой урне. Провести полный анализ цепи Маркова.

3. В каждой из двух урн находится по три шара, причем из этих шести шаров три белых и три черных. Случайным образом вытаскивается один шар из первой урны, один – из второй и они меняются местами. Состояние цепи Маркова – число белых шаров в первой урне. Провести полный анализ цепи Маркова.