2014-02-18
642
1. Закон распределения двумерной дискретной случайной величины (x,h) задан в таблице
| h x | ||||
| -1 | 0,02 | 0,03 | 0,09 | 0,01 |
| 0,04 | 0,20 | 0,16 | 0,10 | |
| 0,05 | 0,10 | 0,15 | 0,05 |
Найти: а) E (x / h); б) E (h / x); в) E (x /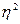 
); г) E (h / 
).
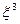2. Пусть независимые случайные величины x и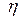 
имеют распределение Пуассона с параметром l каждая. Найти:
а) E (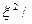
x + h = k);
б) условное распределение P (x = k / x + h = n).
3. Пусть случайные величины x и 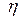имеют совместную плотность распределения 
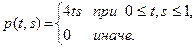. Найти E (x / h).
4. Пусть h 1, h 2, …, hn произвольные случайные величины. Показать, что последовательность xk = hk -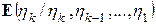 
, k = 1,2,…образуют мартингал.
