Биения. Уравнение биений

Для практики особый интерес представляет случай, когда два складываемых гармонических колебания одинакового направления мало отличаются по частоте w₁ ≈ w₂. Получим уравнение результирующего колебания для этого случая.

Примем, что амплитуды складываемых колебаний равны А, а частоты: w₁ = w, w₂ = w + Δw, причём Δw «w. Начало отсчёта выберем так, чтобы начальные фазы обоих колебаний были равны нулю:

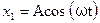(30)

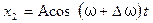
Складываем эти выражения, применяя формулу суммы косинусов.

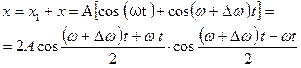
Учитывая, что Δw «w и, пренебрегая Δw в сравнении с w, получаем:

.

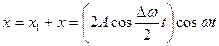Из анализа полученного выражения видно, что сомножитель, стоящий в скобках, меняется гораздо медленнее, чем второй сомножитель. И пока сомножитель в скобках совершит один полный цикл своих изменений, второй сомножитель сделает несколько колебаний.

Это даёт основание рассматривать результирующее колебание х как гармоническое с частотой w и амплитудой А_б, которая изменяется по периодическому закону:

_.

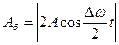Такие изменения амплитуды называются биениями.