2014-02-18
1401
Рассмотрим случай сложения двух гармонических взаимно-перпендикулярных колебаний одинаковой частоты w, совершающихся вдоль координатных осей х и у. Для простоты, начальный момент времени выберем так, чтобы начальная фаза одного из складываемых колебаний равнялись нулю.
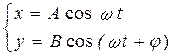(34)
j – разность фаз между колебаниями х и y.
Для момента времени t1 положение тела, участвующего в обоих колебаниях, в системе координат (XOY) будет определяться радиус–вектором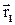 
. В следующий момент t2, координаты х и y примут новые значения, следовательно, и 
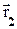изменится и по величине, и по направлению. Уравнение траектории движения тела в координатной плоскости ХОY найдем исключив из (34) параметр t:
;
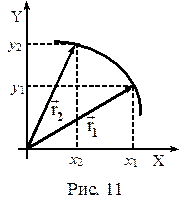
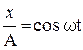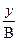= cos(ωt + φ) = cosωt· cosφ + sinωt·sinφ
Т.к.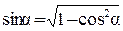 
, то с учётом этого получим:
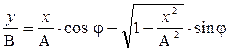
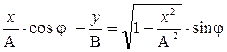
Возведём правую и левую часть последнего равенства в квадрат:
.
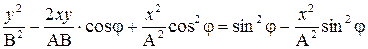Перенесём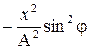 
в левую часть и вынесем за скобки 
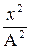, получим:
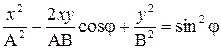. (35)
Из курса математики известно, что это уравнение эллипса в общем случае. Ориентация осей эллипса и его размеры зависят от амплитуд А и В складываемых колебаний и разности фаз j.
Рассмотрим некоторые частные случаи формы траектории результирующего движения, представляющие физический интерес:
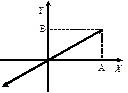1) j = 0; 
; 
 |
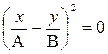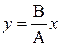
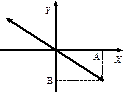2) j = ±p;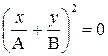 
; 
 |
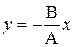
3) 
; 
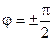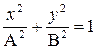
При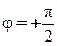 
– движение по траектории по часовой стрелке, если 
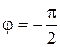– движении против часовой стрелки.
Если частоты складываемых взаимно–перпендикулярных колебаний не одинаковы, то траектории результирующего движения имеют более сложный вид и называются фигурами Лиссажу.
