Сложение колебаний с различными частотами. Биения

Kогда складываются колебания с различными частотами, то наибольший интерес представляет случай мало отличающихся частот. Пусть 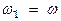, а 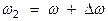, при этом 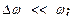. полагаем также, что 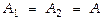и 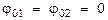. Ур-ние результирующего колебания таково: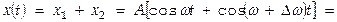 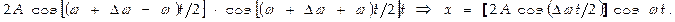Как следствие условия 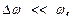за то время, пока множитель 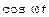совершит несколько полных колебаний, стоящий в квaдрaтныx скобках множитель почти не изменится. Поэтому результирующее колебание м-но рассматривать как гармоническое с частотой 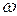, амплитуда к-рого изменяется по нек-рому периодич. закону, т.е. амплитуда результирующего колебания будет равна 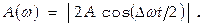Временной хoд этого колебания изображен на рис. 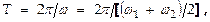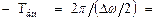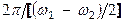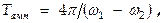Период результирующего колебания а период изменения амплитуды или т.е., 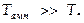Полученное результирующее колебание называют биением.

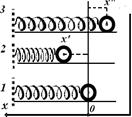
Пружинный маятник. Итак, если в процессе гармонич. колебания МТ движется вдоль оси х, то ее координата при таком движении д-на подчиняться закономерности, описываемой 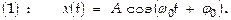Рассматривается пружинный маятник, а это уже — тело массы m, движущееся горизонтально без трения за счет упругости пружины (рис.).

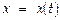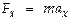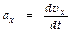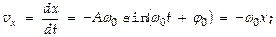
Зная зависимость и массу тела m, нетрудно найти силу, к-рая обеспечивает такое движение (это — 1-ая задача динамики): ; ; ; 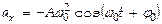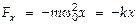, здесь 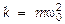¾ постоянная величина, зависящая от характеристик колеблющейся системы. Итак, гармонич. колебания создает сила 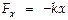, а это и есть упругая сила, подчиняющаяся закону Гука. Теперь м-но написать дифференциальное ур-ние (ДУ), описывающее гармонич. колебания: 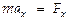или Þ 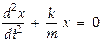; что представляется так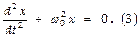

Т.о., гармонич. колебания происходят под действием упругой силы 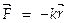(об упругих силах см. также лекцию Mex _03) и описываются ДУ (3). Колебания возникают при деформации растяжения – сжатия некоторого тела, а именно – пружины, и соответствующее периодич. движение происходит вблизи положения равновесия ( положение 1 на рис.).

Физич. систему, колебания к-рой м-но приближенно рассматривать как гармонические, называют гармонич. осциллятором (ГО, это также идеальный образ ¾ модель нек-рого колеблющегося реального тела, рассматриваемого в определенном приближении). Математически временнýю динамику (изменение во времени) такой системы описывают ДУ 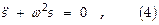здесь 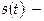переменная, описывающая отклонение нек-рой величины от её равновесного положения 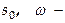частота отклонения. Ур-ние типа (4) ( также — (3)) называют ур-нием гармонич. осциллятора, точнее — линейного ГО (ЛГО)

Кинетич. (W _k) и потенциальная (W) составляющие полной механич. энергии E упругого механического колебания выражаются таk: 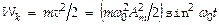и 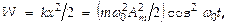t.e., величина полной механич. энергии ЛГО записывается таким образом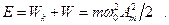

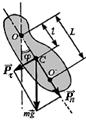
Физическим маятником называют твердое тело, совершающее под действием силы тяжести колебания вокруг горизонтальной оси подвеса, не проходящей через центр масс тела (l – расстояние между точкой подвеса и центром масс).

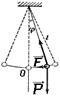При малых углах отклонения (см. рис.): 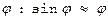движение маятника описывается соотношением 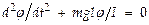— ур-ние ГО для угла отклонения 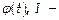момент инерции маятника. Т.о., при малых колебаниях физич. маятник совершает гармонич. колебания 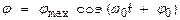с циклич. частотой 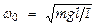и периодом 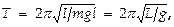где величину 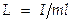называют приведенной длиной физического маятника. Точка O ' на продолжении прямой OC, отстоящая от оси подвеса на расстоянии приведенной длины L, называется центром качаний физич. маятника.

Идеализированную систему, состоящую из МТ массой m, подвешенной на невесомой нерастяжимой нити длиной l и колеблющейся под действием силы тяжести без трения, называют математическим маятником. Реальной моделью математич. маятника может служить небольшой тяжёлый шарик, подвешенный на тонкой длинной нити. Математич. маятник м-но представить как частный (предельный) случай физич. маятника, вся масса к-рого сосредоточена в его центре масс. Уравнение движения математич. маятника тогда м-но получить из ур-ния для физич. маятника, полагая, что 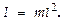Т.е., получают такое соотношение 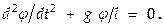Следовательно, движение математич. маятника описывается ДУ типа (3), то есть происходит по закону 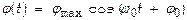с частотой и периодом, соответственно: 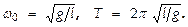Приведенную длину физич. маятника можно определить как длину такого математич. маятника, к-рый имеет такой же период колебаний, что и данный физич. маятник.

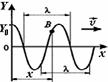
Волновой процесс. Если возбудить колебания в какой-либо точке среды (твердой, жидкой или газообразной) то, вследствие взаимодействия между частицами среды, эти колебания будут передаваться от одной точки среды к другой со скоростью, зависящей от упругих свойств среды. Волновым процессом или волной — называется процесс распространения колебаний в сплошной среде. При распространении волны частицы упруго колеблются около своих положений равновесия, а не перемещаются вслед за волной. Вместе с волной от частицы к частице передается только состояние колебательного движения и его энергия. Основным свойством всех волн является перенос энергии без переноса вещества.

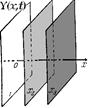Упругая волна называется гармонической, если соответствующие ей колебания частиц среды являются гармонич. Пусть гармонич. волна распространяется со скоростью υ вдоль оси Ox. Обозначим смещение частиц среды от равновесного положения через Y = Y (x, t). Графич. представление волнового процесса дается зависимостью между смещением частиц среды и расстоянием x этих частиц от источника колебаний O в данный момент времени t. Т.е., график волны представляет собой зависимость смещения всех частиц среды от расстояния до источника колебаний в данный момент времени Y = Y (x, t = Сonst), тогда как график гармонич. колебания выражает зависимость смещения данной частицы от времени Y = Y (x = Сonst, t). Длиной волны λ называется расстояние между ближайшими частицами, колеблющимися в одинаковой фазе. Длина волны равна расстоянию, на которое распространяется гармонич. 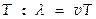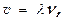волна за время, равное периоду колебаний или где 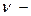частота колебаний, υ — скорость распространения волны. Волновым уравнением называют ДУ, описывающее волновой процесс. Для волны, идущей в направлении Ox, это ур-ние записывается наиболее просто: 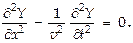Его решение 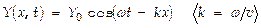(волновая функция) отвечает плоской бегущей волне (w = 2p n - циклич. частота, k - волновое число). Бегущими волнами называют волны, к-рые переносят в пространстве энергию (в отличие от стоячих волн - волн, образуемых наложением встречных волн одной частоты w). Для плоской волны характерен плоский волновой фронт (см. рис. ®). Волновым фронтом называют геометрич. место точек, до к-рых доходят колебания к определенному моменту t. Волновой поверхностью называется геометрич. место точек, колеблющихся в одинаковой фазе. Волновых поверхностей м-но провести бесчисленное множество, а волновой фронт в каждый момент времени — один.