Динамика вращения материальной точки. Автомобиль на выпуклом мосту

Здесь присутствуют интересные и важные особенности.

Если выбирать обычную неподвижную систему координат, то при вращении направления скоростей и ускорения точки будут постоянно изменяться относительно координатных осей.

В расчётах выбирают, так называемую, следящуюсистему координат – систему, начало которой совпадает в выбранный момент времени с движущейся материальной точкой (т.0), а направления ее осей совпадает с направлением скорости тела в этот момент времени (ось абсцисс) и с направлением по радиусу к центру вращения (ось ординат).

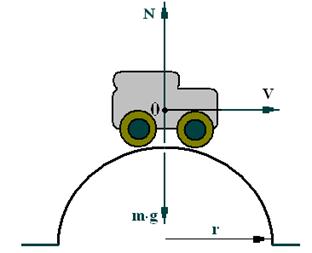
Рассмотрим в качестве примера движение автомашины по выпуклому мосту, радиус которого равен r. Направим одну из осей следящей системы координат к центру моста, а другую – вдоль направления скорости v.

Уравнение движения в этом случае имеет вид (в проекции на вертикальную ось):

ma_ц = mg - N, (1)

где а_ц – центростремительное ускорение,

N – сила реакции моста, mg - сила тяжести.

Решая это уравнение относительно N, получаем, что

N = mg - ma_ц = m(g – 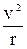). (2)

Откуда следует, что при 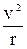= g сила реакции моста будет равна 0.

Но это означает, что автомашина в этот момент времени не оказывает никакого давления на мост, т.е. она находится в состоянии невесомости.

4. Примеры расчёта тяговых усилий при буксировке автомобиля.

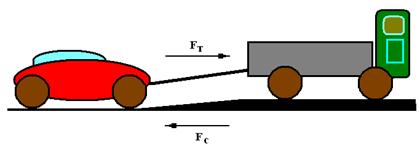
Пример №1.

Автомобильный тягач буксирует автомобиль с заблокированными колёсами. Вес буксируемого автомобиля 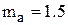тонн. Тягач развивает достаточно большое тяговое усилие. Определить величину силы, начиная с которой буксируемый автомобиль придёт в движение, если коэффициент сухого трения между колёсами автомобиля и поверхностью дорожного покрытия составляет ~ .

Решение.

Буксируемый автомобиль представляется механической системой, на которую действует сила тяги – 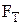и сила сопротивления – .

Последняя представляет собой силу сухого трения – 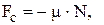где 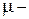коэффициент сухого трения (по условию – 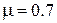), 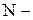нормальная сила давления автомобиля на поверхность дороги (может быть принята равной весу автомобиля, то есть, 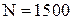кг по условию).

С помощью второго закона Ньютона составляем уравнение движения буксируемого автомобиля:

.

Очевидно, движение должно иметь место при 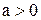. Как видно из уравнения движения, это возможно, когда его правая часть больше нуля, то есть, 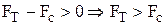. С учётом чисел в условии получаем, что буксируемый автомобиль начнёт движение, когда сила тяги 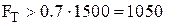кГ!

Задание. Перейти к единицам системы СИ!

Пример № 2.

В условиях предыдущего примера считать, что тяговый трос выполнен из витой сталистой проволоки и может рассматриваться как упругая пружина с коэффициентом упругости – кг/м. Определить величину удлинения троса в момент начала движения буксируемого автомобиля.

Решение.

Сила упругости пружины – удлинение пружины [м].

Очевидно, что в момент начала движения трос должен испытывать действие силы кГ, то есть, 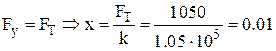м.

Задание. Перейти к единицам системы СИ!

Килограмм-сила (кгс или кГ) равна силе, сообщающей телу массой один килограмм ускорение 9,80665 м/с²

1 кгс = 9,80665 ньютонов (точно^[1]) ≈ 10 Н