2014-02-18
383
Примечание.
Соответственно рисунку слева, модуль векторного произведения, то есть собственно величина момента, определяется произведением –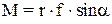 
, а направлениемомента даётся определением правой тройки векторов 
.
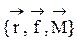Определение 2.
Моментом –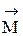 
силы – 
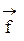, приложенной в точке т.А, относительно произвольной оси 
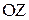называется векторное произведение радиуса-вектора 
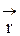и составляющей силы 
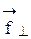, лежащих в плоскости, перпендикулярной оси 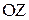и проходящей через точку т. А:
.
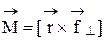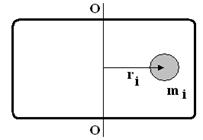
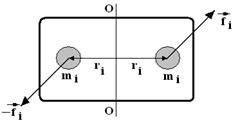
Пусть имеется твердое тело произвольной формы, которое может вращаться вокруг оси ОО. Разбивая тело на малые элементы, можно заметить, что все они вращаются вокруг оси ОО в плоскостях, перпендикулярных оси вращения с одинаковой угловой скоростью – «w».
Движение каждого из отдельных элементов малой массы mi описывается вторым законом Ньютона.
Для i -го элемента имеем:
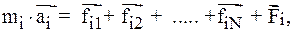(1)
 |
где fik (k = 1,2,...N) представляют собой внутренние силы взаимодействия всех элементов с выбранным элементом, а Fi - равнодействующая всех внешних сил, действующих на i - элемент.
Умножим обе части уравнения (1) на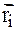 
, получим, что:
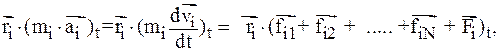(2)
В правой части получившегося уравнения произведения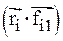 
представляют собой моменты внутренних сил относительно оси вращения. Аналогично, произведения 
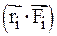являются моментами внешних сил, действующих на i -элемент.
Просуммируем слагаемые в уравнении движения по всем элементам, на которые было разбито тело.
Согласно рисунку, сумма моментов внутренних сил при сложении будет равна НУЛЮ!
Суммарный момент всех внешних сил обозначим –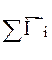 
,где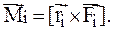 
Левая часть уравнения (2) с учетом соотношения того, что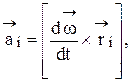 
представляется в таком виде:
= 
=
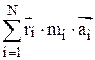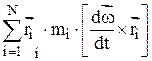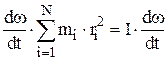, (3)
где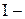 
момент инерции тела.
Уравнение (3) – основное уравнение вращательного движения.
4.Момент инерции твёрдого тела.
Определение 1.
Величина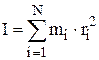 
называется моментом инерции твердого тела
