2014-02-18
426
Равномерное распределение
Распределение Пуассона
Как известно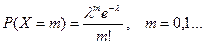 
Ранее мы показали, что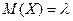 
, воспользуемся формулой 
.
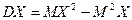Следовательно,
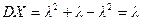(4)
Известно, что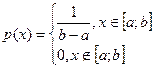 
.
Ранее мы показали, что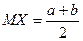 
, воспользуемся формулой .
,
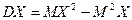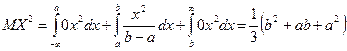тогда
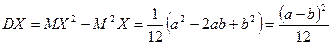. (5)
Определение 1. Начальным моментом k-го порядка случайной величины Х называется число, равное математическому ожиданию случайной величины Хк :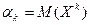 
, k = 1, 2, …
Из этого определения следует, что математическое ожидание случайной величины является начальным моментом 1-го порядка, так как a1 = М(Х).
Определение 2. Центральным моментом k-го порядка называется число, равное математическому ожиданию k-й степени отклонения случайной величины от своего математического ожидания: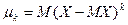 
.
При k = 1,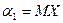 
, 
;
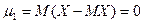при k = 2,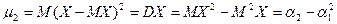 
.
Теорема 1. Если многоугольник распределения дискретной случайной величины или плотность распределения непрерывной случайной величины симметричны относительно прямой х = MX, то все центральные моменты нечетного порядка равны нулю, т.е. m2 к +1 = 0. Докажем это утверждение для непрерывной случайной величины.
