Шкалы
Линейные и круговые шкалы. Отсчетные устройства
Шкалы являются неотъемлемой частью геодезических приборов. Они служат мерами, с которыми сравнивают измеряемые величины.
Шкала представляет собой систему штрихов, нанесенных на какой–либо поверхности и расположенных перпендикулярно к линии шкалы, называемой осевой. В зависимости от формы этой линии шкалы разделяют на линейные и криволинейные. Частным случаем криволинейных шкал являются круговые. Они широко применяются в геодезических угломерных приборах и называются лимбами.
Один из штрихов шкалы принимают за начальный. Он может располагаться по краям шкалы (в линейных шкалах) и в середине (в линейных и круговых – непрерывных шкалах).
Интервал между смежными штрихами шкалы называют делением, а величину τ, равную разности значений двух смежных штрихов xi+1 и xi шкалы, называют ценой деления,
τ =(xi+1 – xi) (43)
Различают шкалы равномерные и неравномерные. В равномерных шкалах штрихи располагаются на равных расстояниях друг от друга. В геодезических приборах чаще применяют равномерные шкалы. Примером неравномерной шкалы могут служить шкалы вольтметров и амперметров.
Для удобства отсчитывания штрихи шкалы подписывают (оцифровывают) через определенные промежутки. Чаще подписывают штрихи, соответствующие целому числу единиц значений, например, сантиметров, дециметров, градусов, минут и т.д. Еще чаще подписывают лишь штрихи, значения которых кратны 5, 10 и т.д. Например, штрихи на лимбах, рассматриваемых при отсчитывании невооруженным глазом или через лупу, обычно подписывают через 5º или 10º. Подписанные штрихи делают обычно длиннее остальных. Иногда для удобства отсчитывания делают несколько удлиненными и некоторые неподписанные штрихи. Например, если удлиняют на лимбе градусные штрихи, то несколько удлиняют и полуградусные.
Если при отсчитывании шкалу рассматривают в микроскоп, то штрихи подписывают так, чтобы в поле зрения микроскопа было видно одновременно не менее двух подписанных штрихов. В некоторых особых случаях допускается, чтобы в поле зрения микроскопа был виден лишь один штрих. Обычно на лимбах, рассматриваемых при отсчитывании в микроскоп, подписывают каждый градус. Направление возрастания отсчетов на лимбах зависит от их целевого назначения и последующих способов обработки угломерной информации. На лимбах для измерения горизонтальных углов оцифровка сделана по часовой стрелке (рис.23, а) по всей окружности. Для вертикальных кругов применяют различные виды оцифровки. Во-первых, оцифровка может быть такой же, как и на горизонтальном круге (рис.23, а). Но на лимб наносят и подписывают градусные деления не по всей окружности, а лишь на участках по 60є. Второй вариант – симметричный (рис.23, б). Причем оба нулевых штриха принимают за начальные. Третий вариант оцифровки (рис.23, в) предусматривает знаки для углов наклона при основном положении вертикального круга: плюс (зрительная труба направлена вверх) и минус (зрительная труба направлена вниз). В высокоточных теодолитах вертикальный круг используется для измерения зенитных расстояний и имеет особенности в оцифровке делений.
Лимбы современных оптических угломерных приборов изготавливаются в форме стеклянного кольца 1 (рис.23, г), которое с помощью прижимного кольца 2 крепится к корпусу 3. Корпус 3 с лимбом 1 насаживают либо на вертикальную ось вращения всего прибора, либо на горизонтальную ось вращения зрительной трубы в зависимости от назначения лимба.
Все современные теодолиты имеют стеклянные угломерные круги, на которых нанесены круговые шкалы – лимбы. Современное оборудование позволяет делить круги с высокой точностью – около 1". Условия, в которых должна находиться делительная машина: располагаться на изолированных фундаментах в отдельных специальных оборудованных помещениях на первом этаже или в подвальной части здания с кондиционированным воздухом.
По мере развития технологии становится возможным изготавливать лимбы более прогрессивными методами: методом прецизионной фотолитографии, методом нанесения штрихов и цифр на лазерном построителе, управляемом ЭВМ. Государственным стандартом для каждого типа теодолита установлена определенная точность деления угломерных кругов. Точность характеризуется полной погрешностью диаметров (под погрешностью диаметров понимают полусумму погрешностей положения штрихов, отстоящих один от другого на 180°).
Действительные значения погрешности диаметров в новых теодолитах не превышают значений, указанных в таблице.
В некоторых случаях погрешности диаметров после установки и закрепления круга в теодолите возрастают. Это может быть следствием деформации круга при закреплении из-за неплоскостности оправы или из-за наличия остаточных внутренних напряжений в стекле, которые вызывают в дальнейшем деформацию круга. Поэтому необходимо исследовать точность разделения кругов нового теодолита, если требуется в дальнейшем выполнять им ответственные и точные работы.
В России освоено нанесение штрихов по лаку методом напыления металла – хрома в вакууме. Внедрение этого метода не только повысило качество штрихов, но и позволило изготавливать угломерные круги с тонкими штрихами (шириной 0,002 мм и менее).
К угломерным кругам предъявляют жесткие требования в отношении чистоты полировки поверхностей, особенно к тем, на которые нанесены штрихи. Например, в зоне штрихов, в пределах участка поля зрения, при увеличении микроскопа 65х – 70х допускаются точки диаметром до 0,002 мм – не более трех.
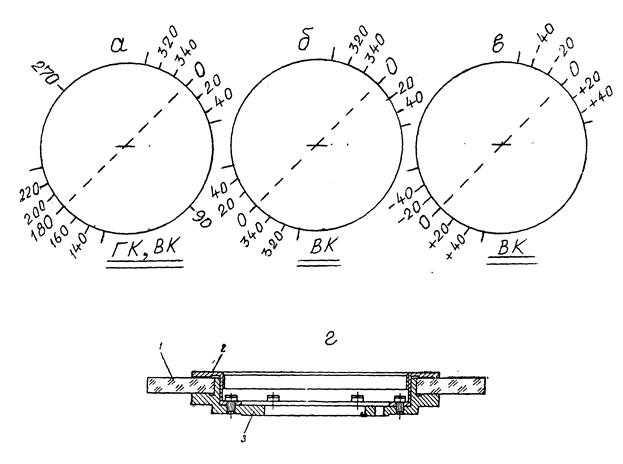
Рис. 47. Виды оцифровки лимбов геодезических приборов
К настоящему времени теоретически разработан, экспериментально опробован и применяется на практике ряд средств и методов автоматизации угловых измерений [5]. Основой автоматизации служат лимбы (диски) с закодированными шкалами градусных делений и специальные устройства для считывания закодированной информации, ее обработки и хранения.
Вся совокупность средств и методов автоматизации угловых измерений по принципу считывания направлений и углов подразделяется на две группы: позиционные и накопительные (импульсные).
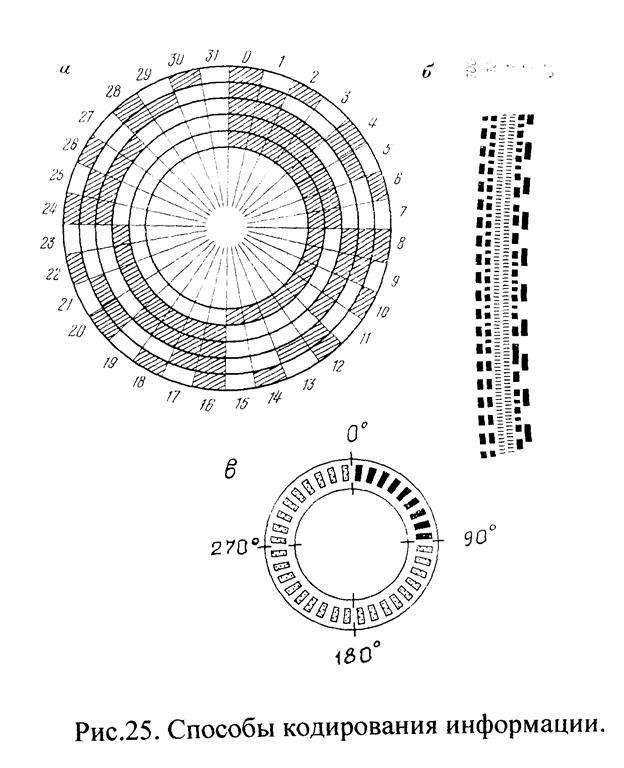
Позиционные средства (иногда называемые абсолютными) отличаются тем, что с диска (лимба) может быть считано любое направление (позиция) в градусной (градовой) мере. Для этого на диске делают несколько дорожек, на которых в определенном коде черно–белыми отрезками кодируют угломерную шкалу (рис.25, а). Количество дорожек (разрядов) зависит от требуемой точности считывания информации. При этом каждый разряд (дорожка) соответствует строго определенному виду информации: сотни градусов, десятки градусов, тактовая дорожка и т.д. (рис.25, б). Горизонтальный угол получается как разность отсчетов (позиций) двух направлений визирования по аналогии с классическим методом полуприемов.
Накопительные (импульсные) средства автоматизации, называемые иногда относительными, базируются на использовании импульсных дисков (рис.25, в), несущих на себе маску последовательно чередующихся элементов «да» и «нет», имеющих одинаковый размер и подсчитываемых электронными счетчиками. Идея импульсного способа измерения углов состоит в том, что величина угла (горизонтального или вертикального) определяется числом импульсов (квантов, элементов кода, инкрементов), укладывающихся на дуге окружности, заключенной между двумя сторонами угла. Размер (цена деления) одного импульса зависит от числа N импульсов, расположенных по окружности диска, и равен τ =360º/N. Иногда этот способ автоматического измерения углов называют накопительным, имея в виду тот факт, что величина угла получается как сумма импульсов (инкрементов), заключенных в его дуге. Возможны два варианта измерения углов, идентифицируемых с классическими. Первый способ приемов – угол получается как разность числа импульсов от произвольно расположенного нуля до правого направления угла и числа импульсов до левого направления. Второй – способ повторений – нуль диска, соответствующий началу счета импульсов, совмещают с левой стороной угла, а его величину получают с помощью подсчета импульсов, уложившихся между левой и правой сторонами горизонтального угла. При этом импульсы могут быть световыми (оптическими), звуковыми (магнитными) и электрическими. Первые два вида импульсов, в конечном счете, преобразуются в электрические.
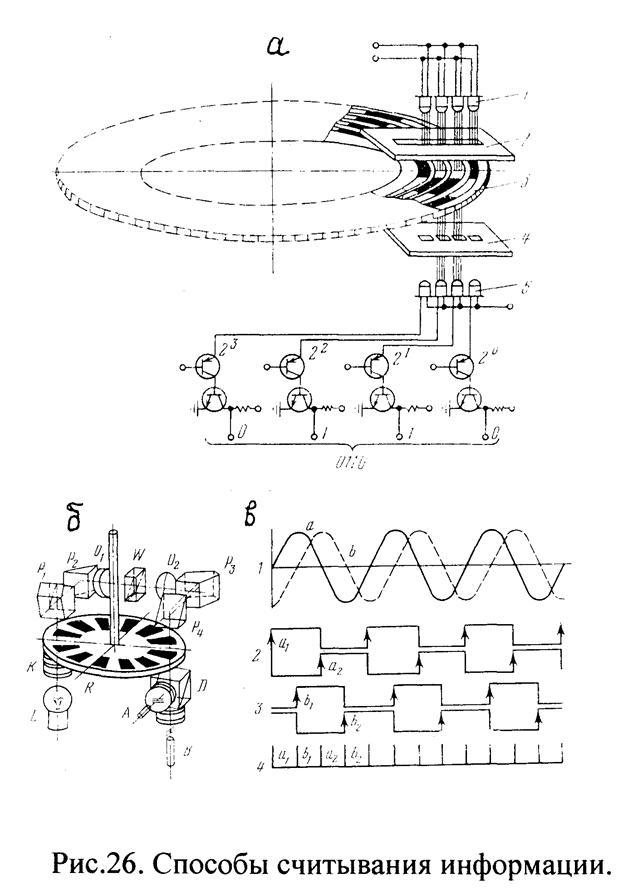
Считывание закодированной информации проводится с помощью механических, индуктивных, магнитных, фотоэлектрических преобразователей и электроннолучевой трубки. В геодезическом приборостроении более рациональными оказались фотоэлектрические преобразователи. Их работа основана на явлениях, возникающих при освещении или затемнении фотоэлементов. Кодовая маска в этом случае состоит из участков, пропускающих и не пропускающих свет, и наносится на стеклянные диски или линейки. В сущности, любой фотоэлектрический преобразователь (рис.26) состоит из источника света 1, ограничивающей 2 и считывающей 4 щелей блока фотоэлементов 5. Количество фотоэлементов соответствует числу дорожек кодового диска 3. Иногда для формирования более узкого пучка света используют цилиндрические линзы, устанавливая их между источником света и кодовым диском. От источника света через ограничивающую щелевую диафрагму проходит узкий пучок света, пересекающий маску в радиальном направлении. Прозрачные участки маски пропускают свет, который затем попадает на соответствующий фотоэлемент. На выходе фотоэлемента возникает сигнал, который может быть считан. Непрозрачные участки маски не пропускают света, поэтому на выходах соответствующих им фотоэлементов сигналов не возникает. Комбинация сигналов на всех фотоэлементах позволяет считать информацию в виде двоичного числа в определенном коде (на рис.26, а двоичное число 0110 соответствует числу 06 в десятичной системе счисления). Точность считывания информации с угломерных кругов (дисков) зависит от характера работ и колеблется в довольно широком диапазоне от 0,1" до 1'.
Считывание оптических импульсов отличается более высокой точностью (возможно изготовление диска с 200 штрихами на 1мм дуги) и потому наиболее широко распространено в геодезическом приборостроении. Для получения наивысшей точности обычно увеличивают число импульсов, содержащихся на окружности диска. При этом используют различные механические, оптические, электронные методы и средства. Одним из первых и наиболее удачных решений в этой области является импульсный датчик формы «Лейтц» (Германия). Диск R (рис.26, б) жестко крепится на алидаде и вращается вместе с ней. На нем нанесено 5000 штрихов, ширина которых равна расстоянию между ними. Лампочка L через конденсор К освещает около 200 рисок сетки. Объективы О1 и О2 передают изображение сетки левой части лимба с помощью пентапризм Р1, Р3 и прямоугольных призм Р2, Р4 на диаметрально противоположную часть лимба в масштабе 1:1. Призмы способствуют оборачиванию изображения, так что изображение левой части при вращении лимба движется против движения правой стороны. Благодаря этому, частота фототока удваивается. Призма Волластона W двойным преломлением расщепляет изображение сетки на два. Одно из изображений образовано действительными лучами, другое – мнимыми. Система рассчитана так, что оба изображения сетки диска попадают на диаметральные риски на взаимном удалении Ѕ интервала сетки. Делительная призма D действует как анализатор, делит оба изображения и направляет одно из них на фотодиод А, другое – на фотодиод – В. Электрические токи, возникающие в обоих фотодиодах, оказываются после этого взаимно сдвинутыми по фазе на 90є (рис.26, в). Они попадают в электронную цепь, где триггеры преобразуют синусоидальные сигналы 1 в прямоугольные 2, 3 того же периода. В дифференцирующем блоке появятся импульсы 4, которые после усиления и выпрямления направляются на ввод счетчика импульсов. Поскольку, кроме главных (синусоидальных) сигналов, образуются зеркальные (косинусоидальные) сигналы (в параллельно соединенной триггерной цепи) и вводятся в дифференцирующую цепь, то число импульсов в 2π будет 2·4·N = 40 000, а величина одного импульса интерполируется несколькими частями, что обеспечивает очень высокую точность отсчитывания. Для интерполирования импульсов используются различные средства и методы [5]: эффект Муара, «синусная щель», эффект «огибания препятствий», фазовые решетки и др.
В любом виде считывающих преобразователей обязательно имеется дискриминатор направления, который определяет знак импульса, т.е. направление вращения алидадной части, и решает задачу – прибавить или вычесть импульс из общей суммы.
Современные электронные геодезические приборы обеспечивают точность считывания информации с лимбов до 0,1".


Измерения длин, углов и других величин сопровождаются отсчетами. Отсчетом называют величину отрезка или дуги между нулевым штрихом шкалы и индексом (нуль–пунктом, указателем), соприкасающимся со шкалой или спроектированным на нее. Штрихи шкалы, между которыми расположен индекс, в зависимости от удаления от нуля шкалы называют младшим и старшим (на рис.24, а это соответственно штрихи 8 и 9, 0 и 1). Отсчет по равномерной шкале складывается из двух частей: отсчет целых делений шкалы, заключенных между нулевым делением шкалы и указателем, плюс дробная часть наименьшего деления шкалы, заключенная между ближайшим к указателю младшим штрихом шкалы и указателем:
S = (N+x)λ = Nλ+xλ, (44)
где N – число целых делений шкалы от нуля до индекса;
x – дробная часть деления шкалы;
λ – цена деления шкалы.
Именно для определения дробной части шкалы служат отсчетные приспособления.
Отсчетные устройства необходимы для обеспечения точности прибора. Их проектируют таким образом, чтобы видимая величина наименьшего интервала между делениями шкалы или лимба составляла 1 – 3 мм. В этом случае при достаточной четкости и освещенности изображения штрихов, а также правильном соотношении ширины штрихов с интервалом между ними точность отсчитывания с оценкой доли на глаз составляет 0,05 – 0,1 интервала. Поэтому для пятисекундного теодолита 2Т5К или 3Т5КП величина наименьшего интервала соответственно 1', для теодолита Т30 – 10', для 2Т30 – 5'. В первом случае точность отсчитывания составляет 3 – 6", во втором 30 – 60", в третьем 15 – 30".
Таблица – погрешность диаметров кругов теодолитов
| Теодолит | Средняя квадратическая погрешность измерения горизонтальных углов | Погрешность диаметров кругов | |
| горизонтального | вертикального | ||
| 2Т2, 3Т2КП 2Т5, 2Т5К, 3Т5КП 2Т30 Т30 | 2" | 1,5" 2,5 | 3 – 2" 3,5 |
В угломерных приборах используются следующие отсчетные приспособления: 1) верньеры; 2) штриховые микроскопы; 3) шкаловые микроскопы; 4) микроскопы с оптическими микрометрами; 5) микроскопы с винтовыми микрометрами. Наибольшее распространение получили приспособления 2,3,4.
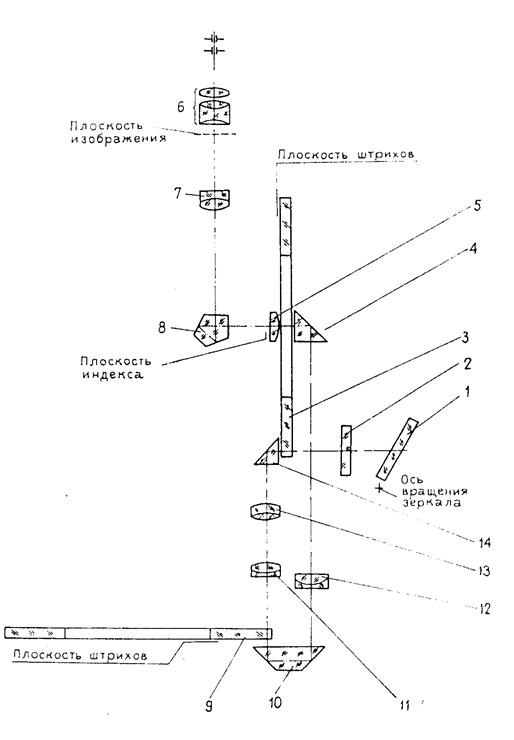
Рис. 50. Оптическая схема отсчетной системы теодолита 4Т30П:
1 – зеркало подсветки; 2 – иллюминатор; 3 – вертикальный круг; 4, 10, 14 – призмы; 5 – коллектив с индексом; 6 – окуляр; 7 – объектив отсчетного микроскопа; 8 – пентапризма; 9 – горизонтальный круг; 11 – вторая линза объектива вертикального круга; 12 – объектив горизонтального круга; 13 – первая линза объектива вертикального круга.
Штриховой микроскоп (микроскоп–оценщик) – это отсчетное устройство, в котором интервал между младшим штрихом лимба и индексом (дробная часть деления шкалы) оценивается на глаз до десятых долей деления лимба. В поле зрения окуляра микроскопа видны одновременно деления горизонтального (Г) и вертикального (В) кругов и отсчетного индекса. Отсчеты берутся по одной стороне круга и соответствуют приведенной выше формуле. На рис., а показаны отсчеты по лимбам
B = 0º30΄+0,6º·10΄ = 0º36΄ и Г = 8º30΄+0,3º·10΄ = 8º33΄, где 10΄ – цена деления лимба.
Схемы передачи изображения горизонтального и вертикального лимбов в поле зрения микроскопа приведены в последующих параграфах при рассмотрении конкретных типов приборов.
Юстировка штрихового микроскопа считается правильной когда:
1) изображения штрихов горизонтального и вертикального кругов четкие;
2) изображения делений кругов находятся в плоскости стеклянной пластинки со штрихом;
3) отсчетный индекс параллелен изображениям штрихов делений лимбов.
Шкаловый микроскоп (рис.24, б) устроен так же, как штриховой, но взамен штриха на стеклянную плоскопараллельную пластинку, расположенную в поле зрения микроскопа, нанесена шкала. Размер шкалы и увеличение микроскопа выбирают так, чтобы видимая величина одного деления лимба точно равнялась длине шкалы. При нарушении этого условия наблюдается рен (от английского – бег, пробег) микроскопа. Влияние рена на результаты измерений, способ его определения и устранения будут рассмотрены далее.
При отсутствии рена полный отсчет по шкаловому микроскопу выражается формулой
S = (Nλ + kγ + yγ), (45)
где N – число целых делений лимба, участвующих в отсчете; λ – цена деления лимба в градусной мере; γ – цена деления шкалы микроскопа; y дробная часть наименьшего деления шкалы, оцениваемая на глаз.
Если шкала имеет n делений, то цену деления шкалы γ можно найти из выражения
γ = λ / n. (46)
На рис.24, б показаны отсчеты В = 0º25,5΄ и Г = 127º05,4΄.
Если шкаловый микроскоп правильно отъюстирован, то выполняются следующие условия:
1) видимые величины наименьших делений как горизонтального, так и вертикального кругов равны общей длине отсчетных шкал микроскопа, т.е. отсутствует рен;
2) штрихи шкал параллельны штрихам делений лимбов;
3) изображения делений лимбов и штрихов шкал при некотором едином положении окуляра микроскопа одинаково четкие.
Двусторонний оптический микрометр (рис. 24, в). Все рассмотренные выше отсчетные устройства позволяют отсчитывать на одном конце диаметра лимба, т.е. не исключают влияние эксцентриситета.
При высокоточных измерениях для исключения влияния эксцентриситета алидады (лимба) отсчитывание производится по двум отсчетным устройствам, расположенным на диаметрально противоположных частях лимба, что вынуждает наблюдателя перемещаться вокруг прибора. Принцип совмещенного отсчитывания позволяет получить отсчет, свободный от эксцентриситета, по одному отсчетному микроскопу. Сущность этого принципа состоит в следующем. С помощью «оптического мостика» рядом с основными штрихами лимба строят прямое (незеркальное) изображение штрихов противоположной части лимба. Затем с помощью оптической системы изображение этих двух частей лимба передается в поле зрения отсчетного микроскопа (рис. 24, в, два левых окошка). При этом младшие штрихи лимба расположатся симметрично относительно мнимого отсчетного индекса (на рисунке его нет) на расстояниях Δ1 и Δ2 от него, не превышающих цену деления лимба λ. То есть Δ1 и Δ2 представляют собой дробные части деления лимба. Тогда отсчет по лимбу можно записать как
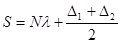 (47)
(47)
Если лимб имеет эксцентриситет, то Δ1 ≠ Δ2, но арифметическое среднее из этих величин свободно от влияния эксцентриситета.
В отличие от предыдущих типов микроскопов в микроскопе–микрометре дробная часть деления лимба не оценивается на глаз и не отсчитывается, а измеряется. С этой целью на пути лучей, проектирующих изображение двух частей лимба в поле зрения микроскопа, устанавливают подвижные оптические детали: плоскопараллельные пластинки, оптические клинья, линзы. Эти детали могут перемещаться в различных направлениях либо поворачиваться вокруг определенных осей под действием специального механизма, снабженного барабанчиком вращения. При перемещении или повороте оптических деталей под действием барабанчика изображения штрихов диаметрально противоположных частей лимба в поле зрения микроскопа будут либо сходиться, либо расходиться в противоположные стороны. Величину смещения штрихов можно отсчитать по шкале, нанесенной на барабанчике. Полный оборот барабанчика от нулевого до последнего деления его шкалы соответствует смещению двух изображений штрихов лимба ровно на одно деление лимба. Поэтому цена деления шкалы микрометра равна
τ = λ / 2n, (48)
где n – количество делений на барабанчике.
Отсчитывание по лимбам производится в таком порядке. В центральном окне поля зрения отсчетного микроскопа (рис. 24, в) находятся изображения диаметрально противоположных бинарных (двойных) штрихов лимба, разграниченные разделительной линией, в верхнем окне – цифры градусов, ниже – шесть цифр (от 0 до 5), указывающих десятки минут, в правом окне – шкала микрометра. Левый ряд цифр шкалы микрометра соответствует единицам минут, правый ряд цифр – десяткам секунд, а каждое деление шкалы – одной секунде.
Перед отсчитыванием, вращая барабанчик микрометра, тщательно совмещают средние линии верхнего и нижнего изображений бинарных штрихов лимба горизонтального (или вертикального) круга. После этого записывают показания шкал. Если в верхнем окне видны два градусных числа, то рабочим является число, находящееся в пределах цифр десятков минут. Цифра, расположенная под серединой числа градусов (2 под 17), показывает количество десятков минут. К ним нужно прибавить единицы минуты (левый ряд цифр – 5), десятки секунды (правый ряд цифр – 2) и единицы секунды со шкалы микрометра (7). На рис. 24, в отсчет соответствует 17º25'27".
а)

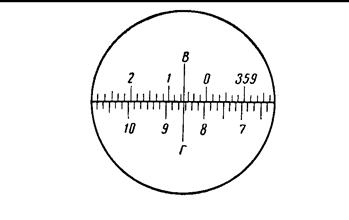

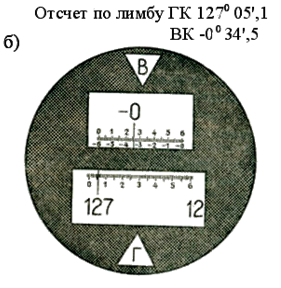
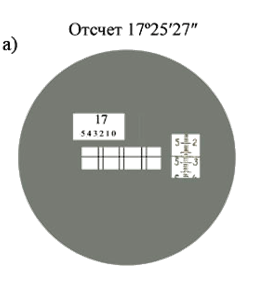
Рис. 51. Поле зрения микроскопа: а) штриховой, б) шкаловый,
в) оптический микрометр
 2014-02-18
2014-02-18 7113
7113








