Барометрическая формула. Распределение Больцмана

Пусть поле тяготения однородно, температура постоянна и масса всех молекул одинакова. Если атмосферное давление на высоте h равно р, то на высоте h+dh оно равно p+dp (при dh>0 и dp<0, так как давление с высотой убывает). Разность давлений р и p+dp равна весу газа, заключенного в объеме цилиндра высотой dh с площадью основания, равной единице площади:

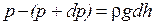, (8.37)

где r – плотность газа на высоте h, далее

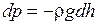. (8.38)

Учитывая, что r = m/V, а рV = (m /m) RТ (m – масса газа, m – молярная масса газа), получаем

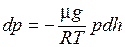, или .

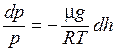С изменением высоты от h ₁ до h ₂ давление изменяется от p ₁ до p ₂, т. е.

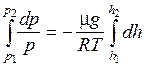, (8.39)

откуда получаем барометрическую формулу

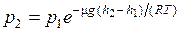. (8.40)

Обычно высоты определяются относительно уровня моря, тогда (8.40) можно записать в виде

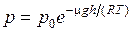(8.41)

где р – давление на высоте h. Используя уравнение состояния p = nkT, получаем

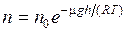, (8.42)

где n – концентрация молекул на высоте h, n ₀ – то же, на высоте h = 0.

Так как m = m ₀ N_A (N_A – постоянная Авогадро, m ₀– масса одной молекулы), а R = kN_A, то

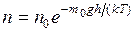, (8.43)

где m ₀ gh = U – потенциальная энергия молекулы в поле тяготения, т. е.

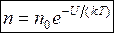. (8.44)

Формула (8.44) выражает распределение Больцмана, откуда следует, что при постоянной температуре плотность газа больше там, где меньше потенциальная энергия его молекул.

Контрольные вопросы

1. Что такое моль?

2. Какой характер имеет взаимодействие молекул идеального газа?

3. Какие вам известны формы записи уравнения идеального газа?

4. Как связано давление газа с энергией поступательного движения молекул, находящихся в единице объема?

5. Чем отличается статистический метод исследования от термодинамического?

6. Почему формула для давления идеального газа на стенки сосуда одинакова для упругого и неупругого столкновений молекул со стенкой?

7. Какие предположения делаются в законе распределения молекул по скоростями и кинетическим энергиям теплового движения?

8. Какие из скоростей молекул больше — средняя или наиболее вероятная?

9. Термодинамическая температура газа изменилась на 1 %. На сколько процентов изменилась при этом средняя скорость молекул?